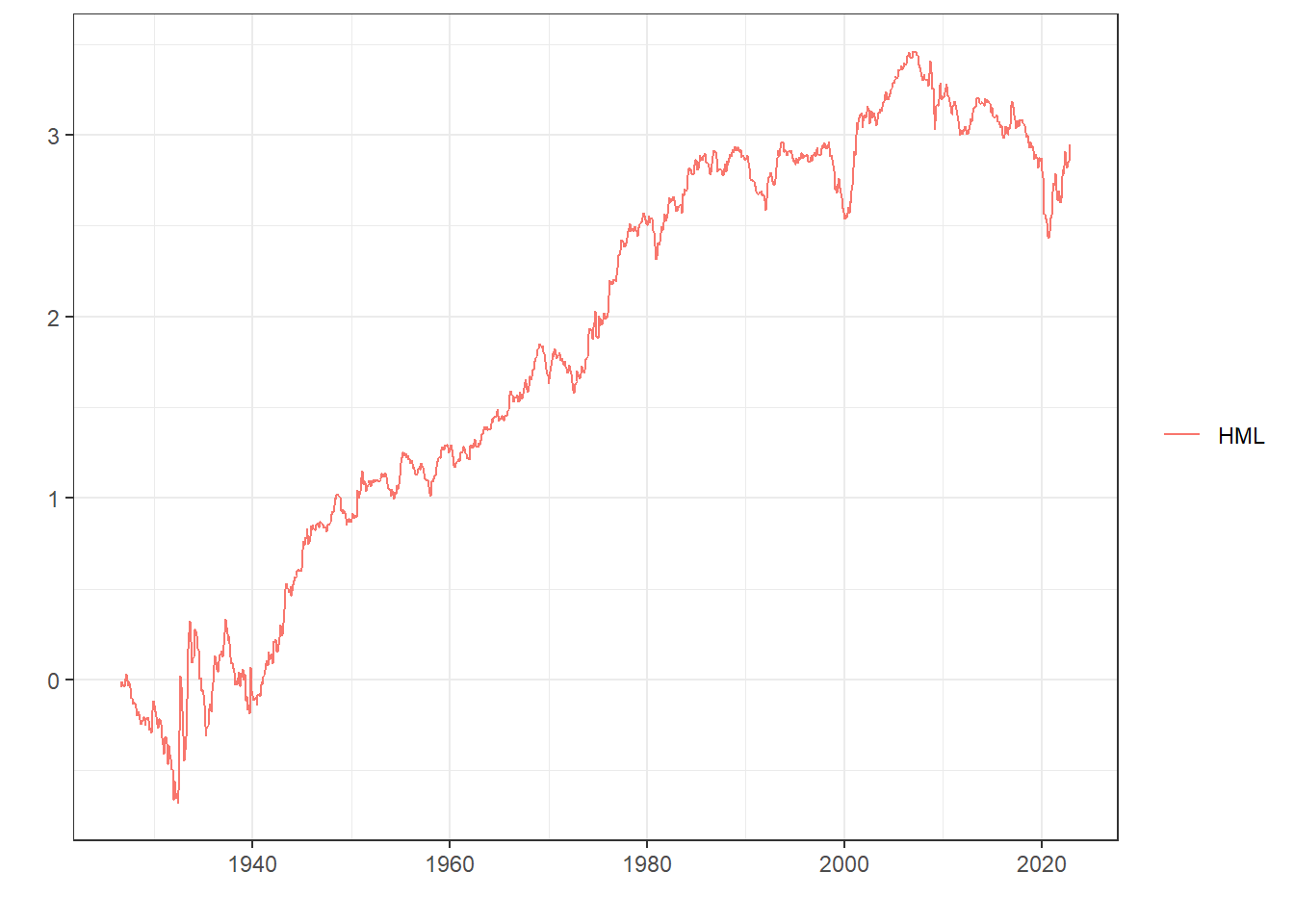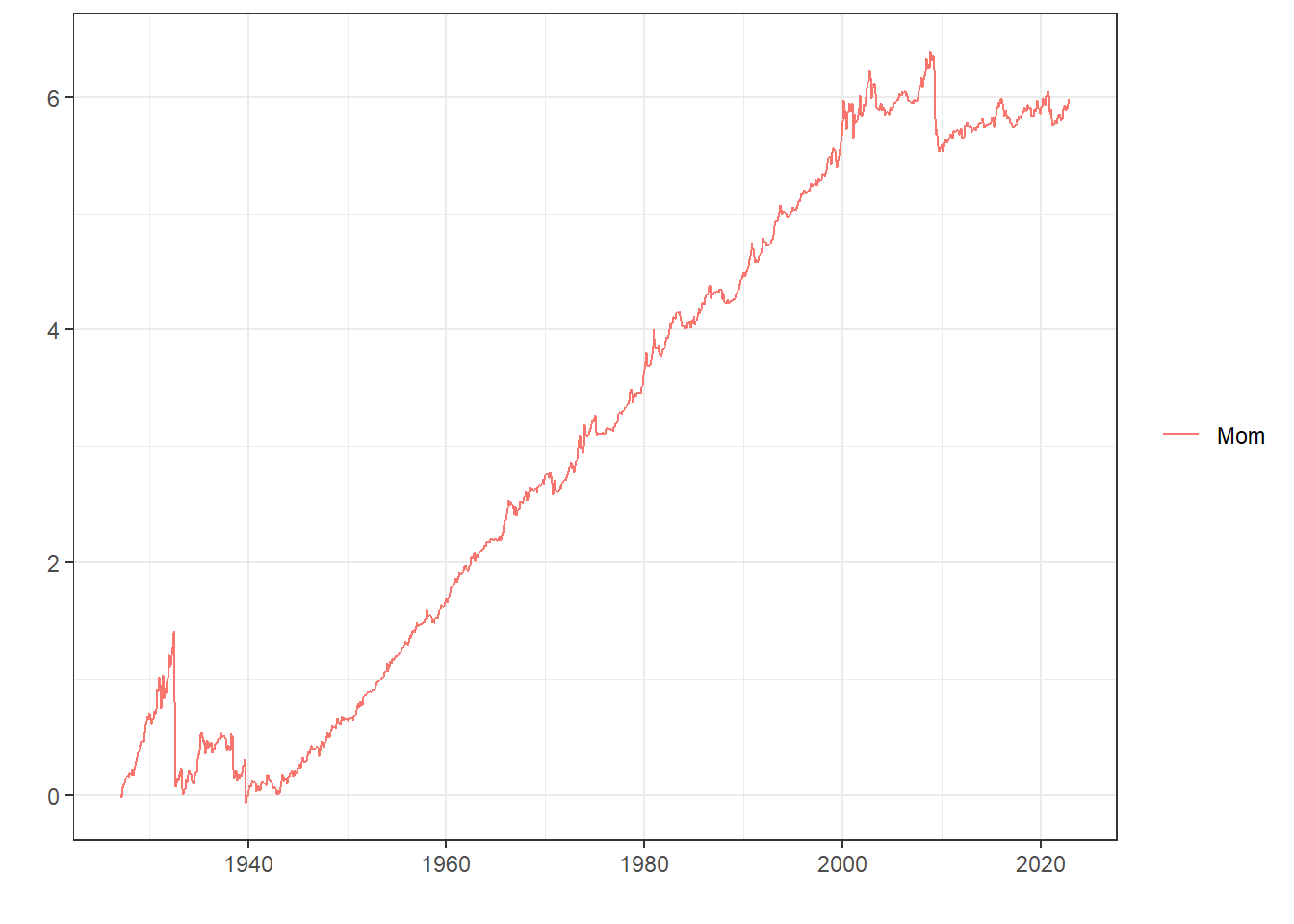퀀트 투자는 크게 포트폴리오 운용 전략과 트레이딩 전략으로 나눌 수 있습니다. 포트폴리오 운용 전략은 과거 주식 시장을 분석해 좋은 주식의 기준을 찾아낸 후 해당 기준에 만족하는 종목을 매수하거나, 이와 반대에 있는 나쁜 주식을 공매도하기도 합니다. 투자의 속도가 느리며, 다수의 종목을 하나의 포트폴리오로 구성해 운용하는 특징이 있습니다. 반면 트레이딩 전략은 주식이 오르거나 내리는 움직임을 연구한 후 각종 지표를 이용해 매수 혹은 매도하는 전략입니다. 투자의 속도가 빠르며 소수의 종목을 대상으로 합니다. 본 수업에서는 퀀트 전략을 이용한 종목선정에 대해 알아보겠습니다.
팩터 이해하기
하나 혹은 소수의 주식만을 연구해서 주식이 오르거나 내리는 공통적인 이유를 찾는 것은 불가능에 가깝지만, 그룹으로 살펴보면 어느 정도 파악이 가능합니다. 어떠한 특성, 예를 들어 기업의 크기 별로 주식들을 묶은 후 수익률을 살펴보면, 크기가 큰 기업의 수익률이 좋았는지 아니면 작은 기업의 수익률이 좋았는지 알 수 있습니다. 즉, 오르는 주식과 내리는 주식은 애초에 가지고 있는 특성이 다르며 그로 인해 수익률에도 차이가 있습니다. 이처럼 주식의 수익률에 영향을 미치는 특성들을 ’팩터(Factor)’라고 하며, 주식의 수익률은 이러한 팩터들로 대부분 설명됩니다. 주식이 가지고 있는 특성만 제대로 알아도 오를만한 주식을 선별하거나, 혹은 내릴만한 주식을 걸러낼 수 있습니다.
그러나 단순히 특성을 기준으로 수익률이 높거나 낮다고 해서 팩터로 인정되는 것은 아닙니다. 팩터로 인정되고 전략으로 사용되기 위해서는 아래의 조건을 충족해야 합니다.
지속성: 오랜 기간, 그리고 여러 경제 상황에서도 꾸준히 작동해야 합니다. 몇 달 혹은 몇 년 동안의 기간에서만 작동한다면 우연의 결과일 가능성이 매우 큽니다.
범용성: 특정 국가에서만 작동하는 것이 아닌 다양한 국가, 지역, 섹터, 자산군에서도 작동해야 합니다. 전세계 중 한국에서만 작동하는 전략이라면 이 역시 우연일 가능성이 큽니다.
이해 가능성: 전략이 작동하는 이유 및 지속 가능한지에 대한 설명이 가능해야 합니다. 수익률이 높은 이유를 경제학이나 이론적으로 설명할 수 있어야 앞으로도 수익률이 높을 것이라 믿을 수 있습니다. 이유가 없는 효과는 우연 혹은 과최적화의 결과일 가능성이 매우 높습니다.
강건성: 같은 팩터라면 비슷한 정의(예: 가치주를 정의하는 PBR, PER, PSR 등) 모두에서 작동해야 합니다. 전략이 작동하는 이유가 명확하다면 정의가 약간씩 달라도 당연히 작동해야 하며, 결과 역시 비슷해야 합니다.
투자 가능성: 이론적으로만 작동하는 것이 아닌 실제로 투자가 가능해야 합니다. 아무리 좋은 전략도 수수료, 세금, 법률적인 문제 등으로 실제 투자가 불가능하다면 돈을 벌 수 없기 때문입니다.
퀀트 운용 전략에서는 팩터의 강도가 양인 종목들로 구성한 포트폴리오는 향후 수익률이 높을 것으로 예상되어 매수를 하며, 팩터의 강도가 음인 종목들로 구성한 포트폴리오는 반대로 향후 수익률이 낮을 것으로 예상되어 매수를 하지 않거나 공매도를 합니다. 기본적인 팩터들에 대해 알아보고, 우리가 구한 데이터를 바탕으로 각 팩터별 투자 종목을 선택하는 방법을 알아보겠습니다.
데이터 불러오기
먼저 샘플로 사용할 주가 및 재무제표 데이터를 다운로드 받습니다. 데이터는 아래 링크에 .sql 파일로 업로드 되어 있습니다.
https://drive.google.com/file/d/13KLFlZTGJvyrlXQYQ_mR0RgAbfYtufti/view?usp=share_link
[다운로드] 버튼을 눌러 파일을 다운로드 합니다. 그 후 SQL에서 해당 데이터베이스를 불러옵니다.
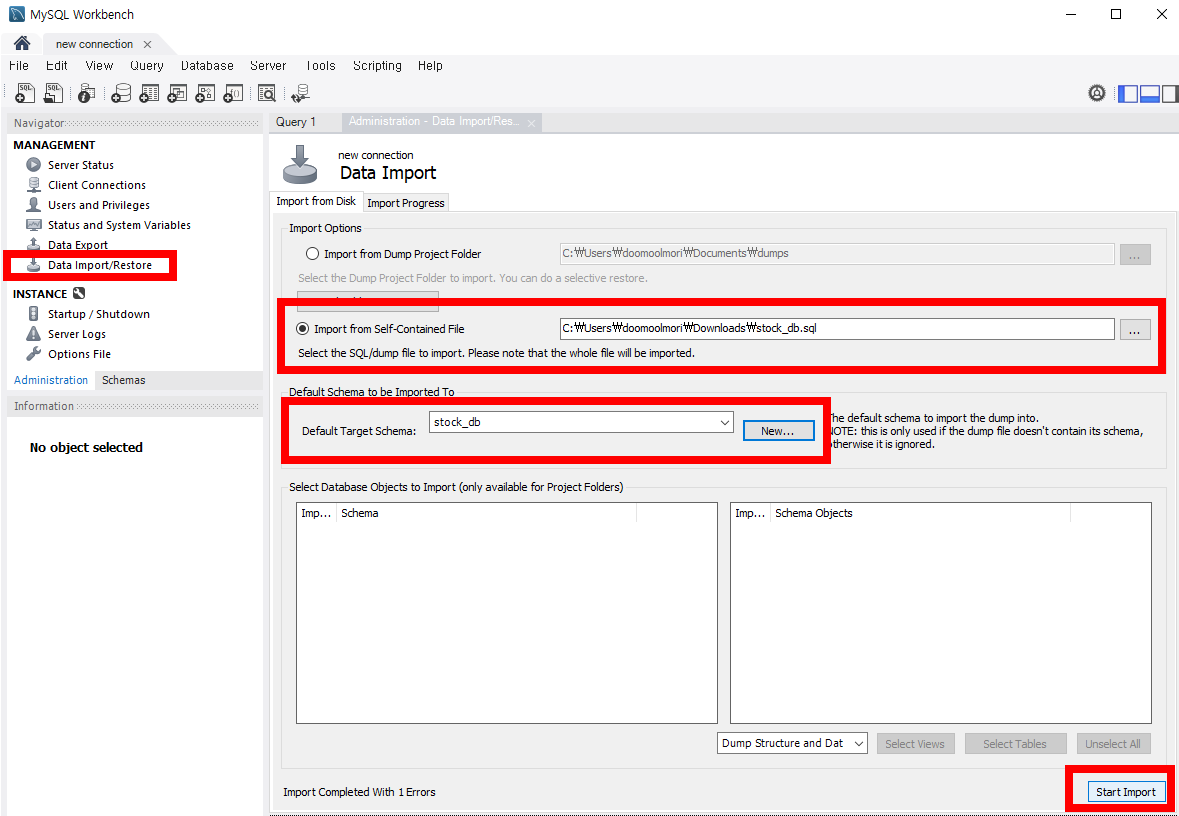
Navigator에서 Administration 부분을 클릭한 후 Data Import를 선택합니다.
Import from Self-Contained File를 선택한 후 […]을 눌러 다운로드 받은 파일을 선택합니다.
Default Target Schema 우측의 New를 누른 후 저장될 데이터베이스 이름을 입력합니다.
하단의 Start Import를 클릭합니다.
데이터베이스를 확인해보면 티커, 주가, 재무제표 데이터가 들어와 있습니다.
밸류 전략
가치주 효과란 내재 가치 대비 낮은 가격의 주식(저PER, 저PBR 등)이, 내재 가치 대비 비싼 주식(고PER, 고PBR)보다 수익률이 높은 현상을 뜻합니다. 가치주 효과가 발생하는 원인은 바로 사람들이 가치주(저밸류에이션)를 기피하고, 성장주(고밸류에이션)를 선호하기 때문입니다. 달리 말하면 사람들이 기피한 주식이 가치주가 되었다고 할 수도 있습니다. 가치주는 일반적으로 차입비율이 높고, 수익의 변동성이 크며, 경기가 좋지 않을 때 더 위험한 경향이 있습니다. 사람들은 이처럼 위험한 주식에 필요 이상으로 과민 반응을 보입니다. 그로 인해 주가가 하락하고 가치주가 되는 것입니다. 반면 인간은 익숙한 것을 안전하다고 착각하는 경향이 있습니다. 최근 성과가 좋은 주식은 여러 매체를 통해 접하기 쉬운데, 이런 주식을 안전하다고 착각해 많은 사람이 매수에 나섭니다. 그로 인해 주가가 상승하고 고평가주가 됩니다. 보고 싶은 것만 보는 확증 편향으로 인해 투자자들은 위험하다고 생각되는 가치주가 망할 것 같은 이유만 찾아 더욱 기피하고, 안전하다고 생각되는 성장주는 영원히 상승할 것 같은 이유만 찾아 더욱 선호합니다. 그러나 가치주가 생각보다 위험하지 않다는 것을, 성장주가 너무 많이 상승해 안전하지 않다는 것을 깨닫는 순간 주가는 원래 수준으로 회귀하기 마련이고, 이로 인해 가치주 효과가 발생합니다.
French Library 데이터 불러오기
파마-프렌치 모형으로 유명한 프렌치 교수가 제공하는 라이브러리에서는 다양한 팩터 데이터를 다운로드 받을 수 있습니다.
https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html
해당 데이터를 분석하기 위해 사이트에 접속하여 데이터를 내려받아 압축을 푼 후 csv 파일을 불러오는 방법 보다는, R 내에서 데이터를 다운로드 받은 후 불러오는 것이 훨씬 효율적입니다. 또한 이미 개발된 패키지를 사용할 경우 이러한 작업을 매우 쉽게 할수도 있습니다.
https://nareal.github.io/frenchdata/articles/basic_usage.html
R에서 해당 패키지를 사용해 팩터 데이터를 다운로드 받은 후 성과를 확인해보도록 하겠습니다.
library (frenchdata)= get_french_data_list ()$ files_list
# A tibble: 297 × 3
name file_url detai…¹
<chr> <chr> <chr>
1 Fama/French 3 Factors ftp/F-F_Research… Data_L…
2 Fama/French 3 Factors [Weekly] ftp/F-F_Research… Data_L…
3 Fama/French 3 Factors [Daily] ftp/F-F_Research… Data_L…
4 Fama/French 5 Factors (2x3) ftp/F-F_Research… Data_L…
5 Fama/French 5 Factors (2x3) [Daily] ftp/F-F_Research… Data_L…
6 Portfolios Formed on Size ftp/Portfolios_F… Data_L…
7 Portfolios Formed on Size [ex.Dividends] ftp/Portfolios_F… Data_L…
8 Portfolios Formed on Size [Daily] ftp/Portfolios_F… Data_L…
9 Portfolios Formed on Book-to-Market ftp/Portfolios_F… Data_L…
10 Portfolios Formed on Book-to-Market [ex. Dividends] ftp/Portfolios_F… Data_L…
# … with 287 more rows, and abbreviated variable name ¹details_url
먼저 필요한 패키지들을 불러온 후, get_french_data_list() 함수를 사용해 다운로드 받을 수 있는 데이터를 조회합니다. data_sets의 files_list에는 다운로드 받을 수 있는데 데이터와 해당 url이 표시되어 있습니다. 이 중 우리는 name 컬럼의 데이터 이름을 알면 됩니다. 이 중 밸류에 해당하는 데이터의 이름은 [Portfolios Formed on Book-to-Market] 입니다. B/M에서 B는 장부가치(Book Value), M는 시장가치(Market Value)로써, 이는 PBR의 역수라고 생각해도 됩니다. 즉 해당값이 높을수록 저PBR 주식을 의미합니다. 해당 데이터를 다운로드 받도록 하겠습니다.
= download_french_data ('Portfolios Formed on Book-to-Market' )
New names:
New names:
New names:
New names:
New names:
New names:
New names:
New names:
• `` -> `...1`
# A tibble: 8 × 2
name data
<chr> <list>
1 Value Weight Returns -- Monthly <spc_tbl_>
2 Equal Weight Returns -- Monthly <spc_tbl_>
3 Value Weight Returns -- Annual from January to December <spc_tbl_ [95 × 20]>
4 Equal Weight Returns -- Annual from January to December <spc_tbl_ [95 × 20]>
5 Number of Firms in Portfolios <spc_tbl_>
6 Average Firm Size <spc_tbl_>
7 Sum of BE / Sum of ME <spc_tbl_ [97 × 20]>
8 Value Weight Average of BE / ME <spc_tbl_ [97 × 20]>
리스트 중 subsets를 확인해보면 월간수익률(시가총액가중평균, 동일가중평균), 연간수익률(시가총액가중평균, 동일가중평균) 및 기타 데이터가 포함되어 있습니다. 이 중 일반적으로 많이 사용하는 시가총액가중포트폴리오의 월간 수익률 (Value Weighted Returns – Monthly)를 확인해보겠습니다.
= ff_value$ subsets$ data[[1 ]]head (ff_value_vw)
# A tibble: 6 × 20
date `<= 0` `Lo 30` `Med 40` `Hi 30` `Lo 20` `Qnt 2` `Qnt 3` `Qnt 4` `Hi 20`
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 192607 12.1 5.55 1.86 1.54 3.18 5.41 1.78 2.41 0.6
2 192608 -9.73 2.65 2.67 5.61 1 4.01 2.05 4.59 7.1
3 192609 -15.2 1.28 0.07 -0.71 -1.04 3.04 -0.29 -0.19 -1.46
4 192610 -5.63 -3.6 -2.41 -3.55 -2.89 -2.96 -2.2 -4.2 -4.28
5 192611 5.58 3.13 2.95 2.94 4.12 2.56 1.9 3.96 2.48
6 192612 -6.13 2.96 2.59 2.52 1.68 3.33 1.82 5.2 2.06
# … with 10 more variables: `Lo 10` <dbl>, `Dec 2` <dbl>, `Dec 3` <dbl>,
# `Dec 4` <dbl>, `Dec 5` <dbl>, `Dec 6` <dbl>, `Dec 7` <dbl>, `Dec 8` <dbl>,
# `Dec 9` <dbl>, `Hi 10` <dbl>
<=0: PBR이 0 이하인 기업들의 포트폴리오
Lo 30, Med 40, Hi 30: PBR 기준 상위 30%, 30-70%, 하위 30%로 나눈 포트폴리오
Lo 20, Qnt 2, Qnt 3, Qnt 4, Hi 20: PBR 기준 상위 20%, 20-40%, 40-60%, 60-80%, 80-100%로 나눈 포트폴리오
Lo 10, Dec 2, Dec 3, …, Dec 9, Hi 19: PBR 기준 상위 10% 씩으로 나눈 포트폴리오
이 중 20%씩 나눈 [Lo 20, Qnt 2, Qnt 3, Qnt 4, Hi 20] 열만 선택하여 누적 수익률을 확인보도록 하겠습니다.
Attaching package: 'dplyr'
The following objects are masked from 'package:stats':
filter, lag
The following objects are masked from 'package:base':
intersect, setdiff, setequal, union
library (tidyr)library (ggplot2)library (lubridate)
Loading required package: timechange
Attaching package: 'lubridate'
The following objects are masked from 'package:base':
date, intersect, setdiff, union
The following objects are masked from 'package:base':
as.Date, as.Date.numeric
= function (data) {%>% mutate (date = as.character (date)) %>% mutate (date = as.Date (as.yearmon (date, "%Y%m" ), frac = 1 )) %>% mutate (across (! date, ~ .x / 100 )) %>% mutate (across (! date, ~ log (1 + .x))) %>% mutate (across (! date, ~ cumsum (.x))) %>% pivot_longer (- date) %>% mutate (name = factor (name, levels = .$ name %>% unique)) %>% ggplot (aes (x = date, y = value, color = name)) + geom_line () + xlab ('' ) + ylab ('' ) + theme_bw () + theme (legend.title= element_blank ())
먼저 데이터를 클렌징한 후 그림으로 나타내는 함수를 만듭니다.
date열을 yyyy-mm-dd로 변경
해당 데이터에서는 1이 1%를 의미하므로, 올바른 계산을 위해 100으로 나누어 줌
로그수익률로 치환
cumsum() 함수를 통해 누적합 계산pivot_longer() 함수를 통해 형태 변경name 열의 순서 지정을 위해 팩터 levels 재설정
그림으로 나타내기
이제 PBR 기준 5분위 열만 선택한 후 해당 함수를 적용합니다.
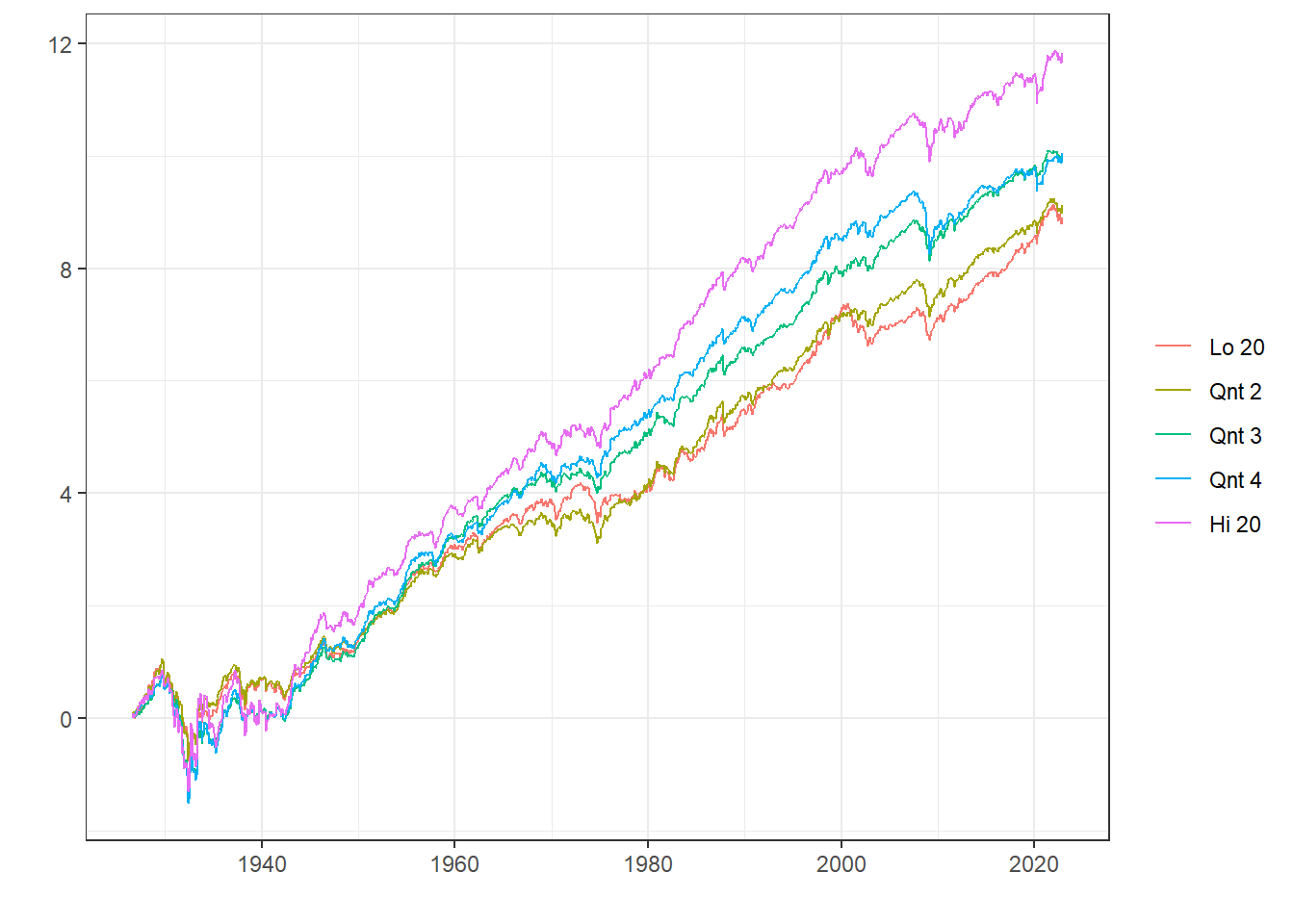
%>% select (date, ` Lo 20 ` , ` Qnt 2 ` , ` Qnt 3 ` , ` Qnt 4 ` , ` Hi 20 ` ) %>% data_to_plot ()
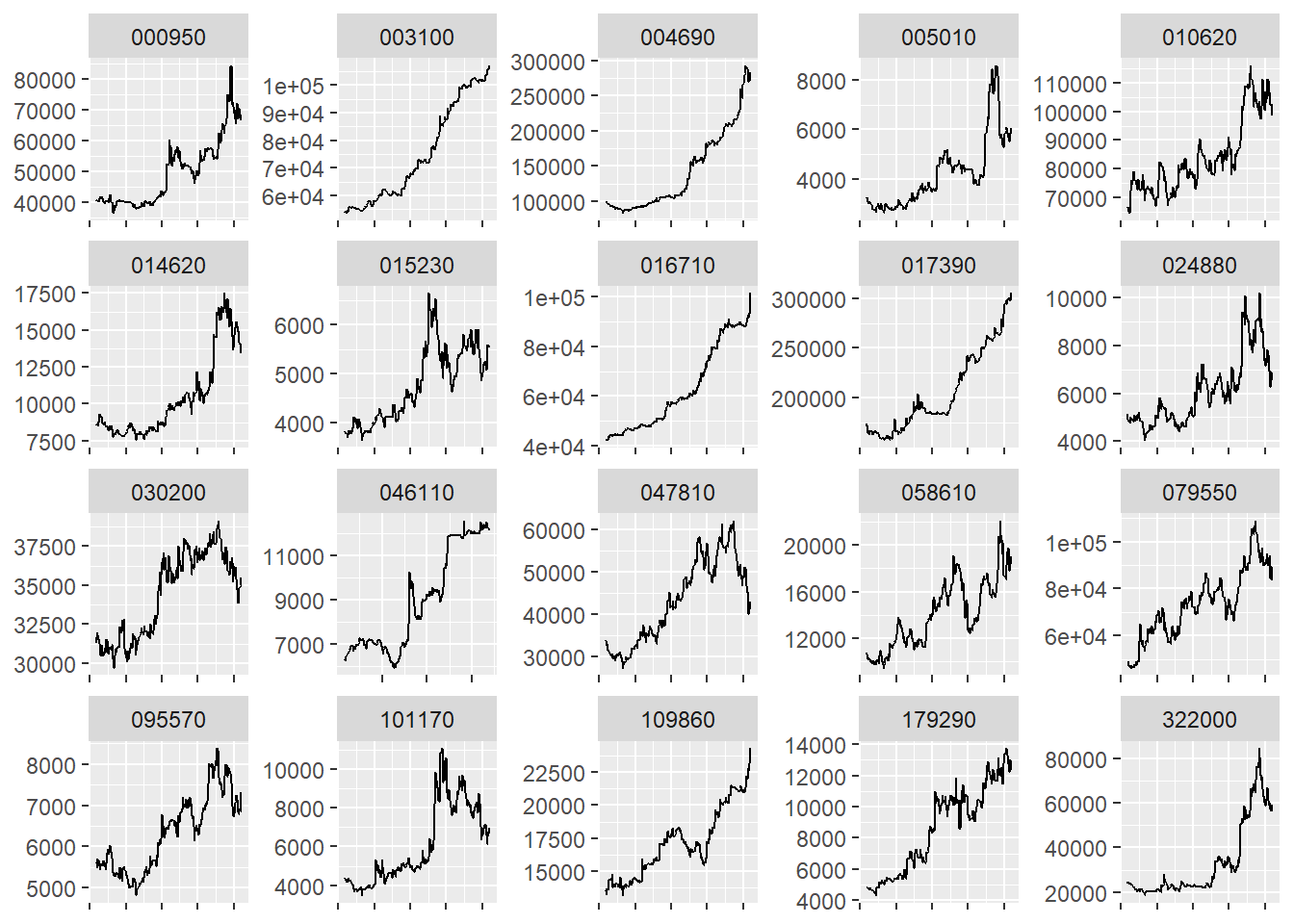
Hi 20, 즉 B/M이 높은(PBR이 낮은) 포트폴리오의 누적 수익률이 가장 높으며, B/M이 낮을수록(PBR이 높을수록) 누적 수익률이 낮아집니다.
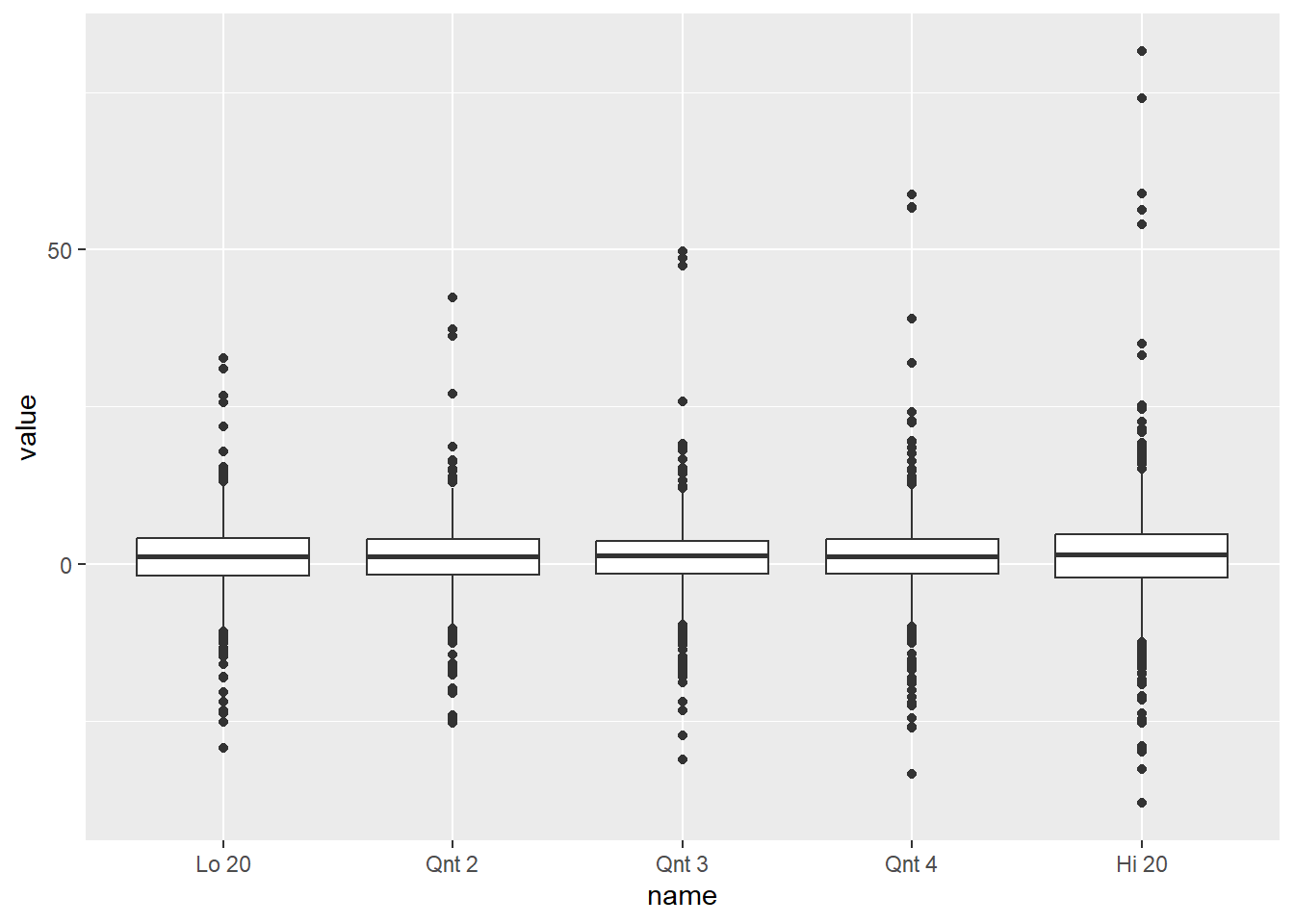
%>% select (date, ` Lo 20 ` , ` Qnt 2 ` , ` Qnt 3 ` , ` Qnt 4 ` , ` Hi 20 ` ) %>% pivot_longer (- date) %>% mutate (name = factor (name, levels = .$ name %>% unique)) %>% ggplot (aes (x = name, y = value)) + geom_boxplot ()
박스 플랏을 분석해 보면 PBR이 낮을수록 수익률의 변동성은 크지만, 큰 수익이 나는 경우가 더 많습니다.
이번에는 고PBR 대비 저PBR 수익률인 HML 팩터의 수익률을 살펴보겠습니다. 흔히 롱숏 모델을 비교할때는 상하위 30% 수익률을 이용합니다.
%>% select (date, ` Lo 30 ` , ` Hi 30 ` ) %>% mutate (HML = ` Hi 30 ` - ` Lo 30 ` ) %>% select (date, HML) %>% data_to_plot ()
1940년 이후 꾸준히 상향하며 저PBR이 고PBR 대비 뛰어난 성과를 기록하였습니다. 반면 2008년 이후 10여년 동안 하락하다가, 2020년을 기점으로 다시 반등하는 모습입니다.
French 라이브러리에서는 PBR외에도 PER나 PCR 팩터의 수익률도 확인할 수 있으며, 미국이 아닌 글로벌 수익률도 확인할 수 있습니다.
밸류 포트폴리오 구하기
가치주에 투자하는 것이 훨씬 수익률이 높다는 점을 확인하였으니, 국내 종목들 중 가치주에는 어떠한 것이 있는 확인해보도록 합니다. 먼저 전통적인 가치지표인 PER와 PBR이 낮은 종목을 선정해보도록 합니다.
library (DBI)library (RMySQL)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , # 위에서 설정한 root 비밀번호 host = '127.0.0.1' ,dbname = 'stock_db' # 사용하고자 하는 스키마 = dbGetQuery (con,"select * from kor_ticker where 기준일 = (select max(기준일) from kor_ticker) and 종목구분 = '보통주';" )= dbGetQuery (con ,"select * from kor_value where 기준일 = (select max(기준일) from kor_value); " )dbDisconnect (con)
먼저 DB에서 티커 테이블과 가치지표 테이블을 불러옵니다. 티커는 최신일 기준 및 보통주에 해당하는 종목만 불러오며, 가치지표는 최신일 기준 데이터를 불러옵니다.
= value %>% mutate (값 = ifelse (값 <= 0 , NA , 값)) %>% pivot_wider (names_from = '지표' , values_from = '값' ) %>% select (- 기준일)= ticker %>% left_join (value)
종목코드 종목명 시장구분 종가 시가총액 기준일 EPS 선행EPS
1 000020 동화약품 KOSPI 8650 2.41607e+11 2022-10-14 647 NA
2 000040 KR모터스 KOSPI 599 5.75869e+10 2022-10-14 NA NA
3 000050 경방 KOSPI 10800 2.96085e+11 2022-10-14 872 NA
4 000060 메리츠화재 KOSPI 29600 3.36798e+12 2022-10-14 5768 6808
5 000070 삼양홀딩스 KOSPI 63800 5.46401e+11 2022-10-14 30711 NA
6 000080 하이트진로 KOSPI 24650 1.72879e+12 2022-10-14 1031 1984
BPS 주당배당금 종목구분 DY PBR PCR PER PSR
1 12534 180 보통주 0.0208 0.6718 5.7117 12.5185 0.7600
2 385 0 보통주 NA 1.1705 NA NA 0.4359
3 30033 125 보통주 0.0116 0.3900 4.7602 15.1838 0.7365
4 22086 620 보통주 0.0209 1.8143 2.7349 4.1457 NA
5 226314 3000 보통주 0.0470 0.2223 3.3317 2.8518 0.1653
6 15657 800 보통주 0.0325 1.5829 4.2258 18.0647 0.7408
일부 종목은 가치지표가 0보다 작은 경우(예: 적자기업의 경우 PER가 음수, 혹은 배당수익률이 0%인 종목)가 있으며 이러한 데이터는 NA로 변경합니다.
테이블을 가로로 긴 형태로 변경합니다.
두 테이블을 합칩니다.
이제 PER와 PBR이 낮은 종목을 찾아보도록 합니다.
%>% mutate (across (c (PBR, PER), min_rank, .names = "rank_{col}" )) %>% mutate (rank = min_rank (rank_PBR + rank_PER)) %>% filter (rank <= 20 )
종목코드 종목명 시장구분 종가 시가총액 기준일 EPS
1 000880 한화 KOSPI 24000 1.79901e+12 2022-10-14 9781
2 001390 KG케미칼 KOSPI 21450 2.97428e+11 2022-10-14 5749
3 001940 KISCO홀딩스 KOSPI 12150 1.96543e+11 2022-10-14 8106
4 002030 아세아 KOSPI 110500 2.42108e+11 2022-10-14 56785
5 003380 하림지주 KOSDAQ 6630 7.42597e+11 2022-10-14 4129
6 006200 한국전자홀딩스 KOSPI 1155 5.40576e+10 2022-10-14 531
7 007860 서연 KOSPI 5270 1.23739e+11 2022-10-14 1091
8 008060 대덕 KOSPI 5990 2.03002e+11 2022-10-14 NA
9 009970 영원무역홀딩스 KOSPI 51200 6.98142e+11 2022-10-14 19026
10 023590 다우기술 KOSPI 17150 7.69463e+11 2022-10-14 8693
11 032190 다우데이타 KOSDAQ 13850 5.30455e+11 2022-10-14 3838
12 037400 우리엔터프라이즈 KOSDAQ 2220 5.82158e+10 2022-10-14 899
13 052300 초록뱀컴퍼니 KOSDAQ 570 6.55956e+10 2022-10-14 942
14 088350 한화생명 KOSPI 2020 1.75443e+12 2022-10-14 1455
15 090740 연이비앤티 KOSDAQ 75 1.68446e+09 2022-10-14 1328
16 101360 이엔드디 KOSDAQ 26000 2.75825e+11 2022-10-14 992
17 106240 파인테크닉스 KOSDAQ 2190 3.48715e+10 2022-10-14 983
18 139480 이마트 KOSPI 84900 2.36666e+12 2022-10-14 56152
19 151860 KG ETS KOSDAQ 8410 3.02760e+11 2022-10-14 1389
20 296640 이노룰스 KOSDAQ 19850 1.02064e+11 2022-10-14 813
선행EPS BPS 주당배당금 종목구분 DY PBR PCR PER PSR
1 8821 52527 750 보통주 0.0312 0.0943 0.3589 0.9098 0.0323
2 NA 34343 500 보통주 0.0233 0.1539 1.1798 0.5282 0.0531
3 NA 68463 400 보통주 0.0329 0.1393 4.7589 1.2965 0.1053
4 NA 491013 3000 보통주 0.0271 0.1407 1.2185 1.3473 0.1211
5 NA 27945 100 보통주 0.0151 0.1684 0.6366 1.0822 0.0572
6 NA 2900 0 보통주 NA 0.1777 1.2175 1.5314 0.1492
7 NA 21587 100 보통주 0.0190 0.1320 0.4529 1.9579 0.0451
8 NA 16976 300 보통주 0.0501 0.1455 0.6002 1.6945 0.1296
9 22866 140307 2000 보통주 0.0391 0.2158 1.7153 1.0987 0.1846
10 NA 45679 600 보통주 0.0350 0.1673 NA 1.1148 0.0962
11 NA 24053 300 보통주 0.0217 0.1085 NA 0.7750 0.0619
12 NA 4170 0 보통주 NA 0.2277 0.9153 1.0267 0.0375
13 NA 2655 0 보통주 NA 0.1442 3.9515 1.1137 0.3827
14 556 15004 0 보통주 NA 0.1488 0.4769 1.5061 NA
15 NA 2489 0 보통주 NA 0.0363 0.3584 0.0952 0.0148
16 NA 7068 0 보통주 NA 0.1615 0.1615 0.1615 0.1615
17 NA 2512 25 보통주 0.0114 0.2265 0.7647 0.6086 0.0716
18 14456 369202 2000 보통주 0.0236 0.1873 3.6898 1.3550 0.0866
19 NA 8862 120 보통주 0.0143 0.2211 4.0584 0.6047 0.0734
20 NA 3492 25 보통주 0.0013 0.2438 NA 0.2438 0.2438
rank_PBR rank_PER rank
1 3 38 5
2 20 12 3
3 11 65 7
4 12 68 9
5 31 45 7
6 36 79 17
7 9 117 20
8 17 93 15
9 65 48 16
10 30 50 9
11 5 31 4
12 76 43 19
13 16 49 6
14 19 76 14
15 1 1 1
16 26 2 2
17 73 18 12
18 47 70 18
19 67 17 11
20 89 3 13
# select(종목코드, 종목명, PBR, PER)
min_rank() 함수를 통해 PER와 PBR 열의 순위를 구하며, rank_열 이름으로 저장합니다.앞서 구한 두 열을 합한 후 다시 순위를 구합니다.
순위가 낮은 20종목을 선택합니다. 이는 PER와 PBR이 낮은 종목이라고 볼 수 있습니다.
여러 지표 결합하기
이번에는 가치지표에 해당하는 모든 지표, 즉 PER, PBR, PCR, PSR, DY를 고려한 밸류 포트폴리오를 만들어보도록 하겠다. 먼저 각 지표 별 상관관계를 살펴보도록 합니다.
= value_bind %>% mutate (across (c (PBR, PER, PCR, PSR), min_rank, .names = "rank_{col}" )) %>% mutate (rank_DY = min_rank (desc (DY)))%>% select (contains ('rank' )) %>% cor (., use = 'complete.obs' ) %>% round (., 2 )
rank_PBR rank_PER rank_PCR rank_PSR rank_DY
rank_PBR 1.00 0.49 0.42 0.74 0.41
rank_PER 0.49 1.00 0.53 0.50 0.33
rank_PCR 0.42 0.53 1.00 0.46 0.26
rank_PSR 0.74 0.50 0.46 1.00 0.36
rank_DY 0.41 0.33 0.26 0.36 1.00
PER, PBR, PCR, PSR의 경우 값이 낮을수록 가치주에 해당하지만, DY의 경우 값이 높을수록 배당수익률이 높은 가치주에 해당한다. 따라서 DY는 desc() 함수를 통해 내림차순으로 순위를 매겨줍니다. 비슷한 가치지표임에도 불구하고 서로 간의 상관관계가 꽤 낮은 지표도 있습니다. 따라서 지표를 통합적으로 고려하면 분산효과를 기대할 수도 있습니다.
%>% mutate (rank_sum = rowSums (across (contains ('rank' )))) %>% mutate (rank_final = min_rank (rank_sum)) %>% filter (rank_final <= 20 )
종목코드 종목명 시장구분 종가 시가총액 기준일 EPS
1 000140 하이트진로홀딩스 KOSPI 10050 2.33228e+11 2022-10-14 1529
2 000880 한화 KOSPI 24000 1.79901e+12 2022-10-14 9781
3 001040 CJ KOSPI 71200 2.07740e+12 2022-10-14 8197
4 001390 KG케미칼 KOSPI 21450 2.97428e+11 2022-10-14 5749
5 002030 아세아 KOSPI 110500 2.42108e+11 2022-10-14 56785
6 002990 금호건설 KOSPI 7300 2.69761e+11 2022-10-14 4130
7 003300 한일홀딩스 KOSPI 10250 3.16037e+11 2022-10-14 1462
8 005990 매일홀딩스 KOSDAQ 7130 9.78115e+10 2022-10-14 3575
9 007860 서연 KOSPI 5270 1.23739e+11 2022-10-14 1091
10 008060 대덕 KOSPI 5990 2.03002e+11 2022-10-14 NA
11 009410 태영건설 KOSPI 4580 1.78158e+11 2022-10-14 1920
12 009970 영원무역홀딩스 KOSPI 51200 6.98142e+11 2022-10-14 19026
13 010100 한국프랜지 KOSPI 2220 6.75999e+10 2022-10-14 612
14 013580 계룡건설 KOSPI 17600 1.57184e+11 2022-10-14 17601
15 016450 한세예스24홀딩스 KOSPI 4190 1.67600e+11 2022-10-14 1026
16 034730 SK KOSPI 206000 1.52748e+13 2022-10-14 37408
17 036530 SNT홀딩스 KOSPI 13900 2.26624e+11 2022-10-14 5329
18 078930 GS KOSPI 45950 4.26946e+12 2022-10-14 15304
19 092230 KPX홀딩스 KOSPI 52700 2.22639e+11 2022-10-14 11573
20 267290 경동도시가스 KOSPI 20050 1.18203e+11 2022-10-14 3756
선행EPS BPS 주당배당금 종목구분 DY PBR PCR PER PSR
1 NA 23538 450 보통주 0.0448 0.2128 0.5890 2.6030 0.1004
2 8821 52527 750 보통주 0.0312 0.0943 0.3589 0.9098 0.0323
3 12727 151085 2300 보통주 0.0323 0.1244 0.7088 2.4128 0.0553
4 NA 34343 500 보통주 0.0233 0.1539 1.1798 0.5282 0.0531
5 NA 491013 3000 보통주 0.0271 0.1407 1.2185 1.3473 0.1211
6 2203 18202 800 보통주 0.1096 0.4132 2.0671 2.8100 0.1295
7 NA 44782 550 보통주 0.0537 0.1627 3.6368 2.9509 0.1634
8 NA 26268 150 보통주 0.0210 0.1473 0.8296 2.3741 0.0521
9 NA 21587 100 보통주 0.0190 0.1320 0.4529 1.9579 0.0451
10 NA 16976 300 보통주 0.0501 0.1455 0.6002 1.6945 0.1296
11 NA 17753 350 보통주 0.0764 0.2518 0.6446 4.2419 0.0627
12 22866 140307 2000 보통주 0.0391 0.2158 1.7153 1.0987 0.1846
13 NA 8412 90 보통주 0.0405 0.2529 1.8270 3.1296 0.0589
14 14985 78914 800 보통주 0.0455 0.2109 2.6687 1.3527 0.0564
15 NA 12066 250 보통주 0.0597 0.1796 4.0581 2.9611 0.0522
16 34166 375047 8000 보통주 0.0388 0.2290 1.7970 1.7034 0.1304
17 NA 65710 700 보통주 0.0504 0.1274 2.6537 2.1604 0.1669
18 19446 108672 2000 보통주 0.0435 0.2967 2.3272 1.7018 0.1657
19 NA 208904 3000 보통주 0.0569 0.1607 3.7481 2.9179 0.1744
20 NA 63687 875 보통주 0.0436 0.3095 1.0442 3.9533 0.0632
rank_PBR rank_PER rank_PCR rank_PSR rank_DY rank_sum rank_final
1 60 170 20 83 179 512 3
2 3 38 7 4 364 416 2
3 7 144 31 21 348 551 6
4 20 12 69 20 510 631 7
5 12 68 74 117 423 694 12
6 316 195 136 126 12 785 18
7 28 216 283 184 115 826 19
8 18 140 45 17 556 776 15
9 9 117 12 10 611 759 14
10 17 93 21 127 131 389 1
11 99 347 25 33 44 548 5
12 65 48 112 218 247 690 11
13 100 240 120 28 231 719 13
14 58 69 197 22 169 515 4
15 39 217 320 18 78 672 9
16 77 95 117 129 254 672 9
17 8 125 196 191 130 650 8
18 146 94 155 190 198 783 17
19 25 213 291 205 92 826 19
20 161 326 58 34 197 776 15
모멘텀 전략
투자에서 모멘텀이란 주가 혹은 이익의 추세로서, 상승 추세의 주식은 지속적으로 상승하며 하락 추세의 주식은 지속적으로 하락하는 현상을 말합니다. 모멘텀의 종류는 크게 기업의 이익에 대한 추세를 나타내는 이익 모멘텀과 주가의 모멘텀에 대한 가격 모멘텀이 있으며, 이 중에서 3개월에서 12개월 가격 모멘텀을 흔히 모멘텀이라고 합니다. 즉 과거 12개월 수익률이 높았던 종목이 계속해서 상승하는 현상을 모멘텀이라 합니다.
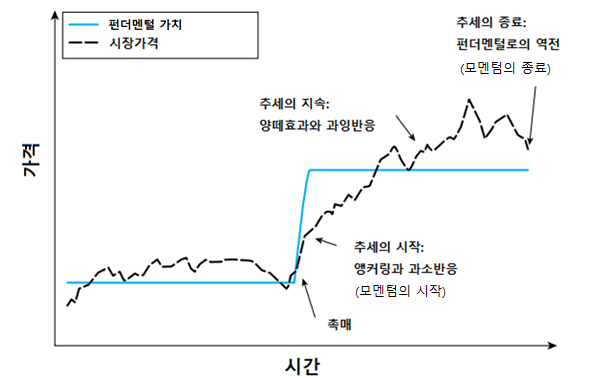
모멘텀 효과가 발생하는 이유는 기업의 가치 변화에 대한 사람들의 반응 때문입니다. 기업의 이익이 증가하면 내재가치(펀더멘털 가치) 역시 증가하고, 이러한 가치는 즉각적으로 변합니다. 반면 주식의 가격은 늘 새로운 정보에 반응해 상승하기는 하지만, 초기에는 이익에 대한 과소 반응으로 인해 상승폭이 낮으며 그 이후 계속해서 상승합니다. 주식의 가격이 가치에 수렴하기 위해 상승하다 보면 투자자들의 주목을 끌기 마련이며, 양떼 효과로 인해 따라서 투자하는 이들이 많아집니다. 그 결과, 과잉 반응이 발생해 주가는 계속해서 상승하며 모멘텀 효과가 발생합니다. 그러나 투자자들이 기업의 가치에 비해 주가가 너무 비싸졌다고 판단하는 순간 주가는 하락하기 시작하며 반전이 이루어집니다.
모멘텀별 포트폴리오의 수익률
프렌치 라이브러리 데이터를 이용해 최근 12개월 수익률을 기준으로 구성된 포트폴리오의 수익률을 비교해보겠습니다.
library (frenchdata)= download_french_data ('10 Portfolios Formed on Momentum' )
New names:
New names:
New names:
New names:
New names:
New names:
New names:
• `` -> `...1`
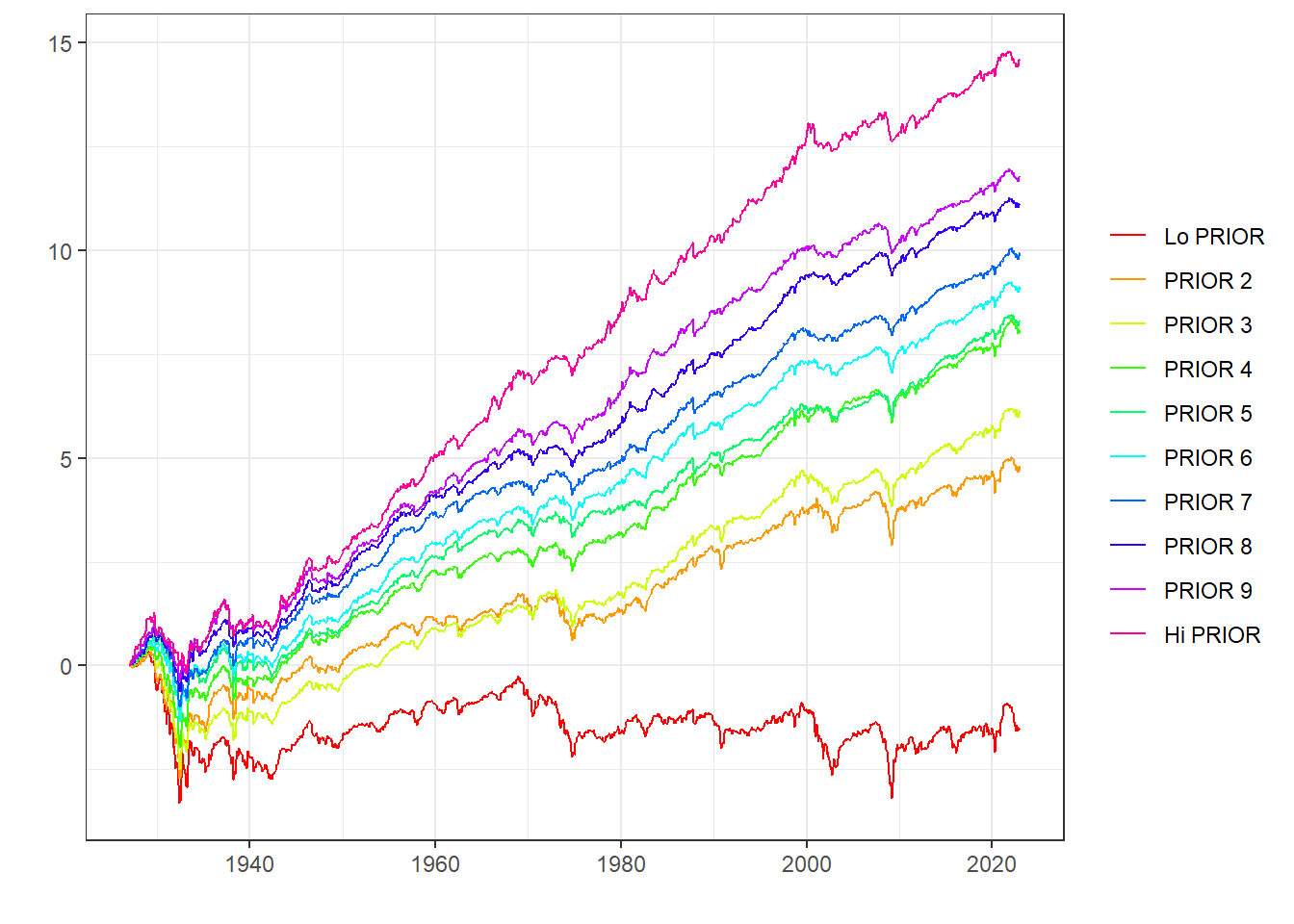
= ff_mom$ subsets$ data[[1 ]]%>% data_to_plot () + scale_colour_manual (values = rainbow (10 ))
모멘텀별 포트폴리오의 누적수익률을 확인해보면, 최근 12개월 수익률이 높을수록(Hi PRIOR) 향후에도 지속적으로 수익률이 높으며, 최근 12월 수익률이 낮을수록(Lo PRIOR) 향후에도 수익률이 낮은 ’모멘텀 현상’이 존재합니다. 이번에는 저모멘텀 대비 고모멘텀 수익률인 UMD 팩터의 수익률을 살펴보겠습니다.
= download_french_data ('Momentum Factor (Mom)' )
New names:
New names:
• `` -> `...1`
$ subsets$ data[[1 ]] %>% data_to_plot ()
장기적으로 우상향 하는 모습을 보이지만 시장이 급락한 이후 반등할 때 모멘텀 팩터가 무너지는 현상이 발생하며, 이를 ’모멘텀 크래쉬’라 합니다.
모멘텀 포트폴리오 구하기
최근 12개월 수익률이 높은 주식에 투자하는 것이 훨씬 수익률이 높다는 점을 확인하였으니, 국내 종목들 중 모멘텀 주식에는 어떠한 것이 있는 확인해보도록 하겠습니다.
library (DBI)library (RMySQL)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , # 위에서 설정한 root 비밀번호 host = '127.0.0.1' ,dbname = 'stock_db' # 사용하고자 하는 스키마 = dbGetQuery (con,"select * from kor_ticker where 기준일 = (select max(기준일) from kor_ticker) and 종목구분 = '보통주';" )= dbGetQuery (con ,"select 날짜, 종가, 종목코드 from kor_price where 날짜 >= (select (select max(날짜) from kor_price) - interval 1 year); " )dbDisconnect (con)= %>% select (날짜, 종목코드, 종가) %>% group_by (종목코드) %>% summarise (ret = last (종가) / first (종가) - 1 )
먼저 티커 테이블과 가격 테이블을 불러옵니다. 가격 테이블은 최근 1년에 해당하는 데이터만 불러옵니다.
가격 테이블에서 종목코드 별로 그룹을 묶습니다.
최근 종가를 1년전 종가로 나누어 1년간의 수익률을 계산합니다.
이제 12개월 수익률이 높은 종목을 찾아보도록 합니다.
= ret_1yr %>% mutate (rank = min_rank (desc (ret))) %>% filter (rank <= 20 ) %>% left_join (ticker)
# A tibble: 20 × 13
종목…¹ ret rank 종목명 시장…² 종가 시가총액 기준일 EPS 선행EPS BPS
<chr> <dbl> <int> <chr> <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl>
1 001570 2.47 5 금양 KOSPI 18650 1.08e12 2022-… 295 NA 2530
2 003610 1.38 15 방림 KOSPI 5780 2.45e11 2022-… 191 NA 5145
3 004690 1.83 8 삼천리 KOSPI 272500 1.10e12 2022-… 17385 NA 392735
4 005860 1.95 7 한일사… KOSDAQ 6260 2.47e11 2022-… 183 NA 1751
5 016710 1.41 14 대성홀… KOSPI 93400 1.50e12 2022-… 1040 NA 29257
6 016790 5.17 2 카나리… KOSDAQ 21100 9.38e11 2022-… NA NA 1876
7 025770 1.01 20 한국정… KOSDAQ 13350 5.00e11 2022-… 295 NA 6019
8 030960 2.99 3 양지사 KOSDAQ 43100 6.89e11 2022-… 96 NA 13794
9 043090 1.13 17 한창바… KOSDAQ 4270 1.88e11 2022-… NA NA 881
10 052020 2.02 6 에스티… KOSDAQ 24750 1.07e12 2022-… NA NA 460
11 053690 1.41 13 한미글… KOSPI 31400 3.44e11 2022-… 1537 2266 14014
12 079810 1.04 19 디이엔… KOSDAQ 10200 1.57e11 2022-… 62 886 1711
13 090710 1.55 11 휴림로… KOSDAQ 2150 3.52e11 2022-… NA NA 443
14 095500 2.82 4 미래나… KOSDAQ 14950 4.64e11 2022-… 940 NA 8392
15 101670 6.87 1 코리아… KOSDAQ 15500 2.98e11 2022-… NA NA 1470
16 179290 1.58 10 엠아이… KOSDAQ 13050 4.19e11 2022-… 392 968 2081
17 249420 1.05 18 일동제… KOSPI 26800 7.18e11 2022-… NA NA 6429
18 322000 1.49 12 현대에… KOSPI 56400 6.32e11 2022-… NA 5743 28600
19 366030 1.26 16 공구우… KOSDAQ 7140 1.57e11 2022-… 581 NA 1797
20 373200 1.75 9 하인크… KOSDAQ 5410 1.02e11 2022-… NA NA 1872
# … with 2 more variables: 주당배당금 <dbl>, 종목구분 <chr>, and abbreviated
# variable names ¹종목코드, ²시장구분
min_rank() 함수를 통해 수익률의 순위를 구하며, 모멘텀의 경우 지표가 높을수록 좋으므로 desc() 함수를 통해 내림차순으로 순위를 구합니다. 마지막으로 해당 종목들의 가격 그래프를 확인해보도록 하겠습니다.
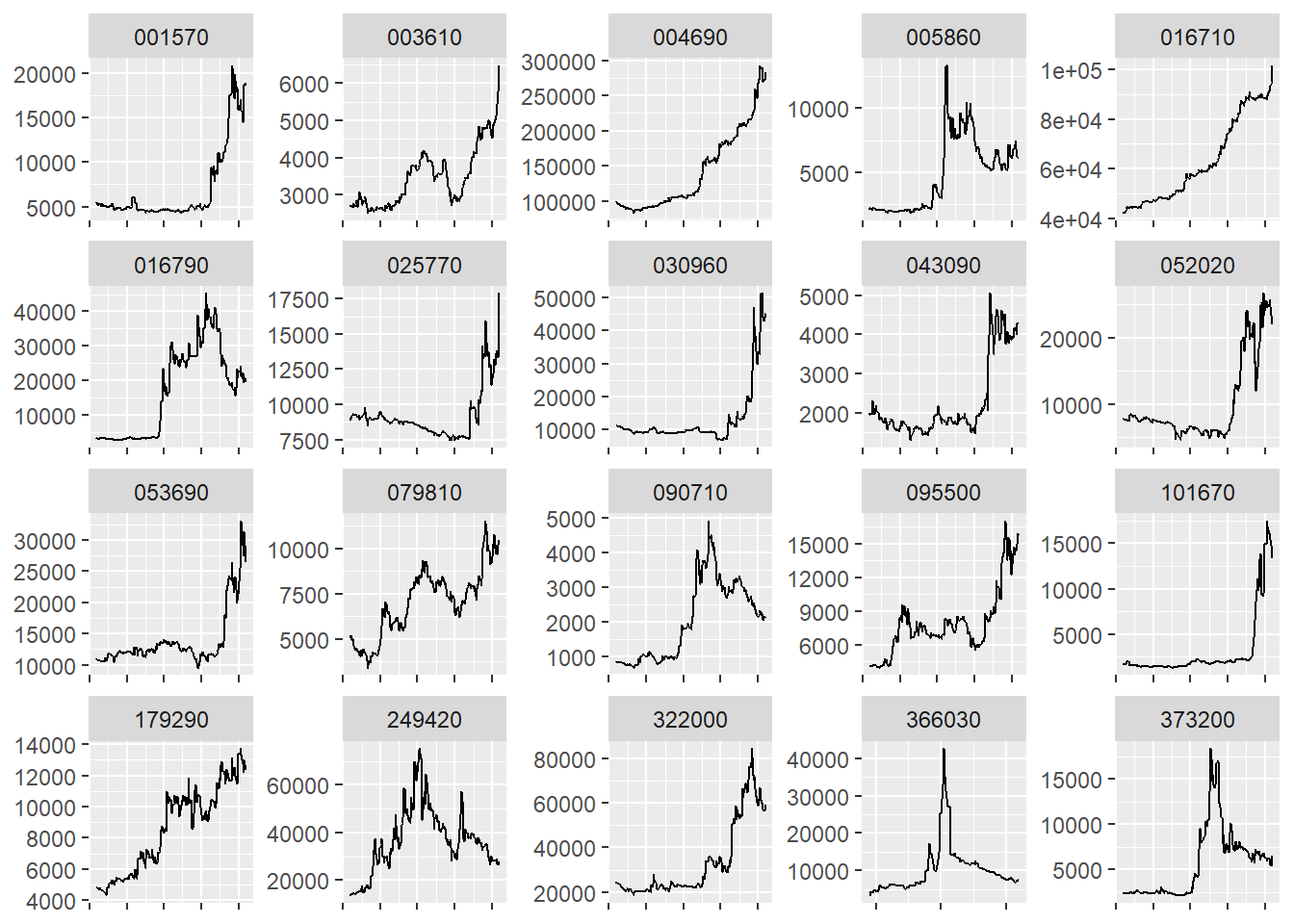
%>% filter (종목코드 %in% (momentum_bind %>% select (종목코드) %>% pull ())) %>% group_by (종목코드) %>% slice_tail (n = 255 ) %>% ggplot (aes (x = as.Date (날짜), y = 종가)) + geom_line () + facet_wrap (. ~ 종목코드, scales = 'free' ) + xlab (NULL ) + ylab (NULL ) + theme (axis.text.x= element_blank ())
K-Ratio
12개월 수익률 기준 모멘텀 종목들의 주가 그래프를 보면 단순히 수익률 만으로 종목을 선택할 경우 다음과 같은 종목 또한 포함됩니다.
장기간 수익률이 횡보하다가 최근 주가가 급등하여 누적수익률 역시 높게 나타나는 종목
이미 몇달전에 주가가 급등한 후 최근에는 하락세이지만, 누적수익률 자체는 높게 나타나는 종목
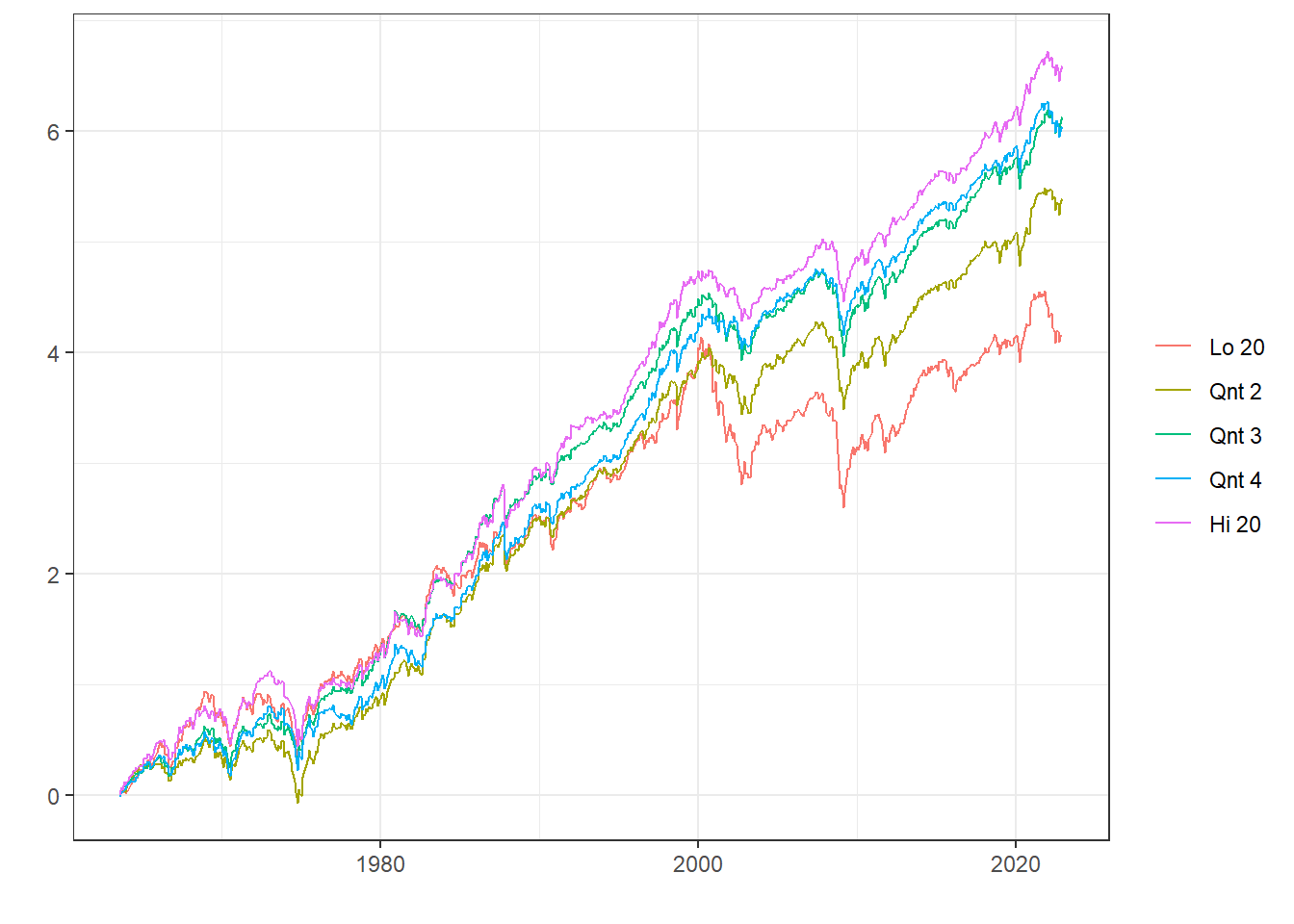
반면 좋은 모멘텀 주식이란 단순히 많이 상승한 것이 아닌, 꾸준하게 상승하는 종목이다. 하나의 예를 살펴봅시다.
동일한 누적수익률을 가진 두 종목이 있다고 가정해봅시다. A의 경우 상승폭이 작다가 최근 급등하여 누적수익률이 높아진 경우입니다. 반면 B의 경우 꾸준하게 상승하여 누적수익률이 높아진 경우입니다. 이 중 꾸준하게 상승한 B가 더 뛰어난 모멘텀 주식이라고 볼 수 있습니다. 이처럼 꾸준한 상승을 측정하기 위해 실무에서는 단순 12개월 수익률이 아닌 3~12개월 수익률을 같이 보거나, 변동성을 함께 고려하기도 합니다. 그 중 모멘텀의 꾸준함을 측정하는 지표 중 하나가 ’K-Ratio’입니다. 해당 지표는 다음과 같습니다.
\[K-Ratio = \frac{누적수익률의\ 기울기}{표준\ 오차}\] 누적수익률이 높을수록 기울기도 커져 분자는 커집니다. 또한 추세가 꾸준할수록 표준 오차가 작아 분모는 작아집니다. 따라서 추세가 꾸준하게 많이 상승할수록 K-Ratio는 증가합니다. 먼저 K-Ratio를 측정하는 법을 살펴봅시다.
library (tidyr)library (broom)= price %>% filter (종목코드 == '005930' ) %>% mutate (ret = 종가 / lag (종가) - 1 ) %>% mutate (ret = log (1 + ret)) %>% slice (- 1 ) %>% mutate (cumret = cumsum (ret)) %>% mutate (id = row_number ()) = lm (cumret ~ id, data = tbl)summary (reg)
Call:
lm(formula = cumret ~ id, data = tbl)
Residuals:
Min 1Q Median 3Q Max
-0.11585 -0.02906 0.01277 0.03074 0.08558
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.200e-01 6.377e-03 18.82 <2e-16 ***
id -1.396e-03 4.458e-05 -31.31 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.04996 on 245 degrees of freedom
Multiple R-squared: 0.8001, Adjusted R-squared: 0.7993
F-statistic: 980.5 on 1 and 245 DF, p-value: < 2.2e-16
먼저 삼성전자에 해당하는 데이터만 뽑아 수익률을 계산합니다.
로그수익률로 변경한 후 로그 누적수익률을 계산합니다.
row_number() 함수를 통해 순서를 입력합니다.lm() 함수를 통해 \(x\) 축에는 기간, \(y\) 축에는 로그 누적수익률로 회귀분석을 실행합니한다.
결과표의 ’Estimate’는 기울기를, ’std err’는 표준 오차를 나타냅니다.
cat (coef (summary (reg))[2 , 1 ],coef (summary (reg))[2 , 2 ],coef (summary (reg))[2 , 1 ] / coef (summary (reg))[2 , 2 ]
-0.001395999 4.458329e-05 -31.31215
기울기와 표준오차를 추출한 후, 이 두개를 나눈 값이 K-Ratio 입니다. 이를 이용해 모든 종목의 K-Ratio를 계산하도록 하겠습니다.
library (purrr)library (broom)= price %>% group_by (종목코드) %>% filter (n () >= 200 ) %>% mutate (ret = 종가 / lag (종가) - 1 ) %>% mutate (ret = log (1 + ret)) %>% slice (- 1 ) %>% mutate (cumret = cumsum (ret)) %>% mutate (id = row_number ()) = step_1 %>% ungroup () %>% nest (data = - 종목코드) %>% mutate (model = map (data, ~ lm (cumret~ id, data = .)),tidied = map (model, tidy))= step_2 %>% unnest (tidied) %>% filter (term == 'id' ) %>% mutate (k_ratio = estimate / ` std.error ` ) # k_ratio = price %>% # group_by(종목코드) %>% # filter(n() == t) %>% # mutate(ret = 종가 / lag(종가) - 1) %>% # mutate(ret = log(1+ret)) %>% # slice(-1) %>% # mutate(cumret = cumsum(ret)) %>% # mutate(id = row_number()) %>% # do({model = lm(cumret ~ id, data = .); # data.frame(slope = coef(summary(model))[2, 1], std_err =coef(summary(model))[2, 2])}) %>% # mutate(k_ratio = slope / std_err) %>% # ungroup()
상장한지 200일 이상 된 종목만 선택합니다.
수익률을 계산합니다.
K-Ratio를 구합니다.
이를 토대로 K-Ratio 상위 종목을 구해보겠습니다.
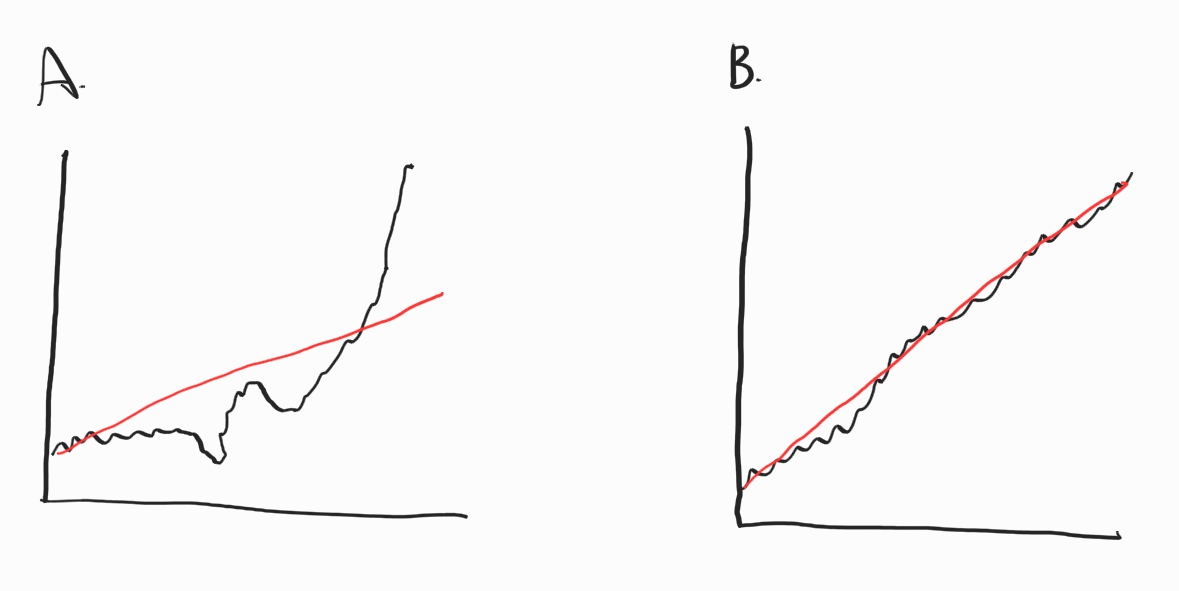
= k_ratio %>% mutate (rank = min_rank (desc (k_ratio))) %>% filter (rank <= 20 ) %>% left_join (ticker)%>% filter (종목코드 %in% (k_bind %>% select (종목코드) %>% pull ())) %>% group_by (종목코드) %>% slice_tail (n = 255 ) %>% ggplot (aes (x = as.Date (날짜), y = 종가)) + geom_line () + facet_wrap (. ~ 종목코드, scales = 'free' ) + xlab (NULL ) + ylab (NULL ) + theme (axis.text.x= element_blank ())
기존 단순 모멘텀이 비해 훨씬 더 꾸준하게 우상향하는 종목들이 선택되었습니다.
퀄리티 전략
벤자민 그레이엄 이후 유지되고 있는 기본적 분석 혹은 가치 투자자들의 가장 중요한 투자 지표 중 하나는 기업의 우량성(퀄리티)입니다. 벤저민 그레이엄은 종목 선정에 있어 유동 자산이 풍부하여 재무적으로 건전하고, 꾸준하게 이익을 달성하는 기업을 강조했습니다. 최고의 투자자로 꼽히는 워런 버핏의 종목 선정 기준 역시 실적의 강력한 성장 추세와 높은 자기자본 이익률로 알려져 있습니다.
그러나 어떠한 지표가 기업의 우량성을 나타내는지 한 마디로 정의하기에는 너무나 주관적이고 광범위해 쉽지 않습니다. 연구에 따르면 수익성, 성장성, 안정성이 높을 주식일수록 수익률이 높은 경향이 있습니다. 이 외에도 학계 혹은 업계에서 사용되는 우량성 관련 지표는 다음과 같이 요약할 수 있습니다.
수익성: 기업이 돈을 얼마나 잘 버는가(ROE, ROA, 매출총이익률 등).
수익의 안정성: 기업이 얼마나 안정적으로 돈을 버는가(ROE의 변동성 등).
재무 구조: 기업의 재무 구조가 얼마나 안전한가(차입비율 등).
이익의 성장: 기업의 이익 증가율이 얼마나 되는가(전년 대비 ROE 증가율 등).
재무 신뢰도: 재무제표를 얼마나 신뢰할 수 있는가(회계 처리 방법 등).
배당: 얼마나 주주 친화적인가(배당금, 신주발행, 자사주 매입 등.)
투자: 얼마나 신사업에 투자를 하는가(총자산의 증가 등)
이 중 사람들이 가장 중요하게 여기는 것은 바로 수익성입니다. 돈을 벌지 못하는 기업은 지속될 수 없기 때문입니다. 기업의 규모가 크면 당연히 돈을 더 많이 벌기 때문에 단순히 수익의 양이 아닌, 기업의 규모에 비해 얼마를 버는지 표준화를 통해 비교해야 합니다.
ROE
자기자본이익률
당기순이익
자본
ROA
총자산이익률
당기순이익
자산
ROIC
투하자본이익률
당기순이익
투하자본
GP
매출총이익률
매출총이익
자산 혹은 자본
우량주 효과가 발생하는 이유 역시 사람들의 반응과 관계가 있습니다. 기업의 수익성이 높을 경우, 투자자들은 이익이 다시 원래 수준으로 빠르게 돌아갈 것이라 생각하지만, 실제로는 수익성이 높은 기업은 계속해서 높은 수익성을 보이는 경향이 있습니다. 반대로 기업의 수익성이 낮은 경우, 투자자들은 이익이 반등할 것이라 생각하지만 나쁜 기업은 계속해서 나쁜 경향이 있습니다.
수익성별 포트폴리오의 수익률
프렌치 라이브러리 데이터를 이용해 영업수익성을 기준으로 구성된 포트폴리오의 수익률을 비교해보겠습니다.
= download_french_data ('Portfolios Formed on Operating Profitability' )
New names:
New names:
New names:
New names:
New names:
New names:
New names:
• `` -> `...1`
= ff_op$ subsets$ data[[1 ]]%>% select (date, ` Lo 20 ` , ` Qnt 2 ` , ` Qnt 3 ` , ` Qnt 4 ` , ` Hi 20 ` ) %>% data_to_plot ()
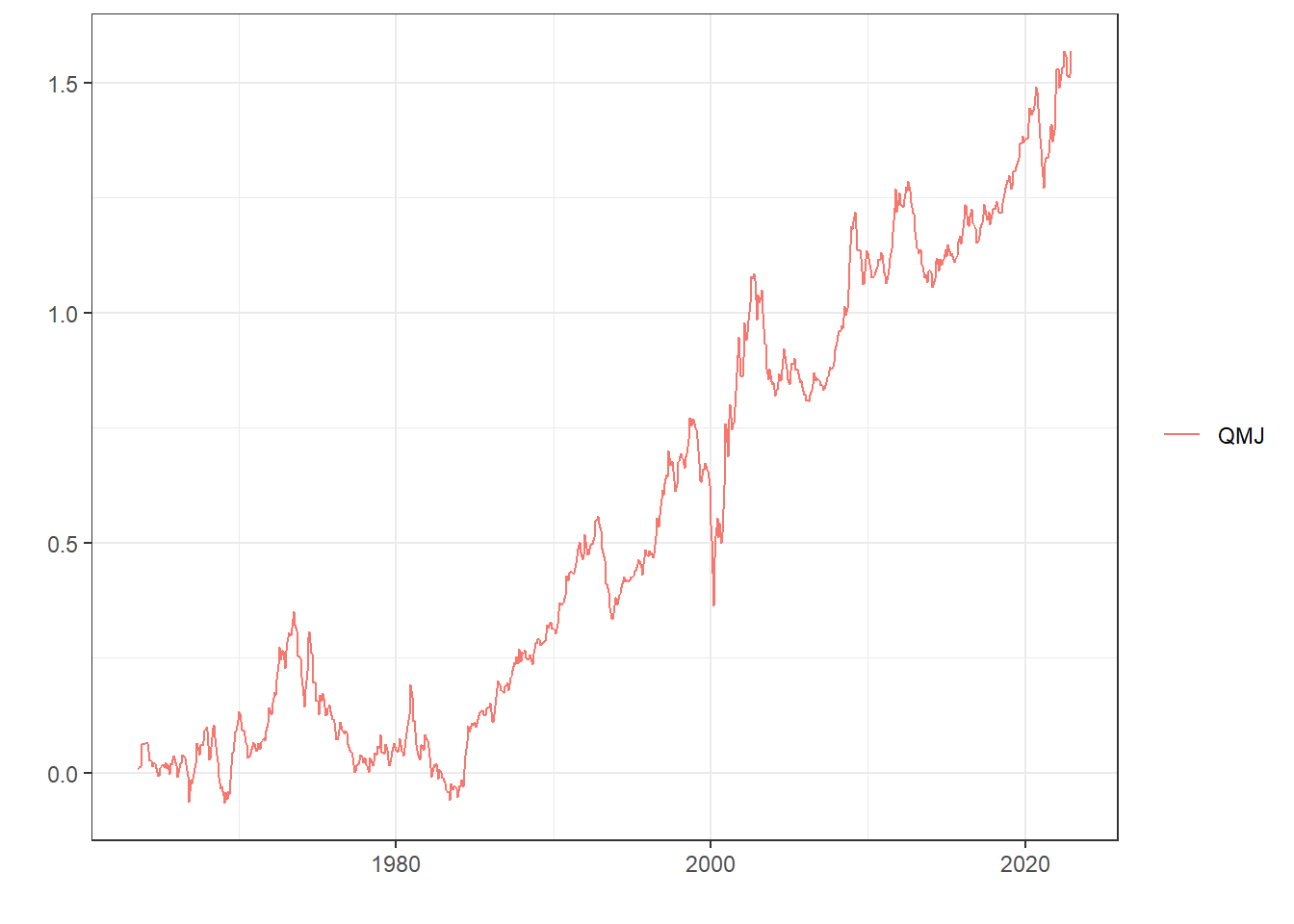
누적수익률을 확인해보면 수익성이 높을수록(Hi 20) 향후에도 지속적으로 수익률이 높으며, 수익성이 낮을수록(Lo 20) 향후에도 수익률이 낮은 ’퀄리티 현상’이 존재합니다. 이번에는 저수익성 대비 고수익성 수익률인 QMJ 팩터의 수익률을 살펴보겠습니다.
%>% select (date, ` Lo 30 ` , ` Hi 30 ` ) %>% mutate (QMJ = ` Hi 30 ` - ` Lo 30 ` ) %>% select (date, QMJ) %>% data_to_plot ()
역시나 장기간 우상향하는 모습입니다.
우량성 포트폴리오 구하기
이번에는 국내 종목들 중 우량성(수익성)이 높은 종믁은 어떠한 것이 있는지 확인해보도록 하겠습니다.
library (DBI)library (RMySQL)library (RcppRoll)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , # 위에서 설정한 root 비밀번호 host = '127.0.0.1' ,dbname = 'stock_db' # 사용하고자 하는 스키마 = dbGetQuery (con,"select * from kor_ticker where 기준일 = (select max(기준일) from kor_ticker) and 종목구분 = '보통주';" )= dbGetQuery (con ,"select * from kor_fs where 계정 in ('당기순이익', '매출총이익', '영업활동으로인한현금흐름', '자산', '자본') and 공시구분 = 'q'; " )dbDisconnect (con)= fs %>% arrange (종목코드, 계정, 기준일) %>% group_by (종목코드, 계정) %>% mutate (rollsum = roll_sum (값, n = 4 , align = 'right' , fill = NA )) %>% slice (n ()) %>% mutate (rollsum = case_when (%in% c ('자본' , '자산' ) ~ rollsum / 4 ,TRUE ~ rollsum%>% ungroup ()
# A tibble: 11,384 × 6
계정 기준일 값 종목코드 공시구분 rollsum
<chr> <chr> <dbl> <chr> <chr> <dbl>
1 당기순이익 2022-06-30 65 000020 q 193
2 매출총이익 2022-06-30 468 000020 q 1666
3 영업활동으로인한현금흐름 2022-06-30 48 000020 q 423
4 자본 2022-06-30 3652 000020 q 3596.
5 자산 2022-06-30 4639 000020 q 4549
6 당기순이익 2022-06-30 12 000040 q -104
7 매출총이익 2022-06-30 42 000040 q 158
8 영업활동으로인한현금흐름 2022-06-30 -2 000040 q -130
9 자본 2022-06-30 479 000040 q 492
10 자산 2022-06-30 1640 000040 q 1698.
# … with 11,374 more rows
티커와 재무제표 테이블을 가져오고, 수익성을 계산하는데 필요한 계정(당기순이익, 매출총이익, 영업활동으로인한현금흐름, 자산, 자본 / 분기 데이터)을 불러옵니다.
종목코드와 계정별로 그룹을 묶은 후, roll_sum() 함수를 이용해 최근 4분기 데이터의 합을 구합니다.
slice(n()) 함수를 통해 그룹에서 가장 최근 데이터만 선택합니다.자산과 자본의 경우 재무상태표 항목이므로 합이 아닌 평균을 구하며, 나머지 항목은 합을 그대로 사용합니다.
이제 각종 수익성 지표를 계산하겠습니다.
= fs_roll %>% select (계정, 종목코드, rollsum) %>% pivot_wider (names_from = 계정, values_from = rollsum) %>% mutate (ROE = 당기순이익 / 자본,GPA = 매출총이익 / 자산,CFO = 영업활동으로인한현금흐름 / 자산)
마지막으로 수익성 지표의 순위를 구한 후, 상위 20 종목을 선택합니다.
%>% mutate (across (c (ROE, GPA, CFO), .fns = ~ rank (desc (.)), .names = "rank_{col}" )) %>% mutate (rank = rank (rank_ROE + rank_GPA + rank_CFO)) %>% filter (rank <= 20 ) %>% left_join (ticker) %>% select (종목명, 종목코드, ROE, GPA, CFO)
# A tibble: 20 × 5
종목명 종목코드 ROE GPA CFO
<chr> <chr> <dbl> <dbl> <dbl>
1 DB하이텍 000990 0.447 0.495 0.339
2 HMM 011200 0.905 0.574 0.570
3 엠게임 058630 0.266 0.703 0.226
4 아프리카TV 067160 0.358 0.739 0.305
5 랩지노믹스 084650 0.520 0.649 0.386
6 이크레더블 092130 0.285 0.647 0.259
7 씨젠 096530 0.402 0.606 0.390
8 위메이드맥스 101730 0.349 0.776 0.260
9 LX세미콘 108320 0.435 0.642 0.281
10 에스디바이오센서 137310 0.466 0.482 0.301
11 파수 150900 0.330 0.699 0.387
12 휴마시스 205470 1.32 1.17 0.932
13 골프존 215000 0.343 0.674 0.295
14 삼양옵틱스 225190 0.348 0.554 0.263
15 수젠텍 253840 0.670 0.574 0.371
16 제이시스메디칼 287410 0.555 0.882 0.258
17 비올 335890 0.291 0.545 0.32
18 넥스틴 348210 0.439 0.640 0.239
19 원티드랩 376980 0.259 0.903 0.269
20 F&F 383220 0.654 1.01 0.315
섹터 중립 포트폴리오
팩터 전략의 단점 중 하나는 선택된 종목들이 특정 섹터로 쏠리는 경우가 있다는 점입니다. 특히 과거 수익률을 토대로 종목을 선정하는 모멘텀 전략은 특정 섹터의 호황기에 동일한 섹터의 모든 종목이 함께 움직이는 경향이 있어 이러한 쏠림이 심할 수 있습니다.
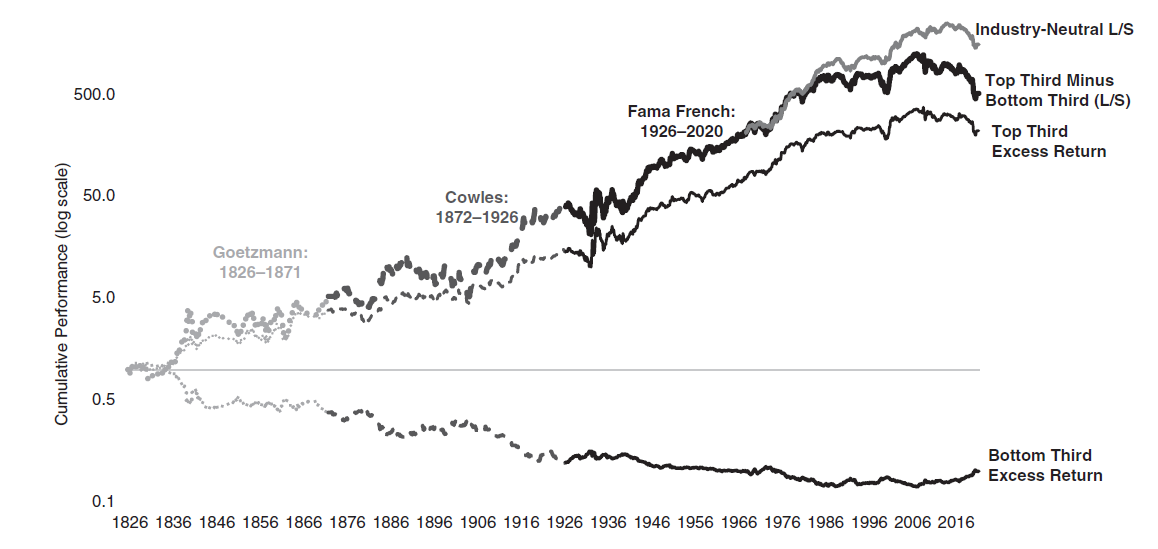
실제 연구 결과를 살펴보아도 섹터 중립 포트폴리오의 수익률이 일반적인 포트폴리오의 수익률 보다 높습니다.
먼저 12개월 모멘텀을 이용한 포트폴리오 구성 방법을 다시 살펴봅시다.
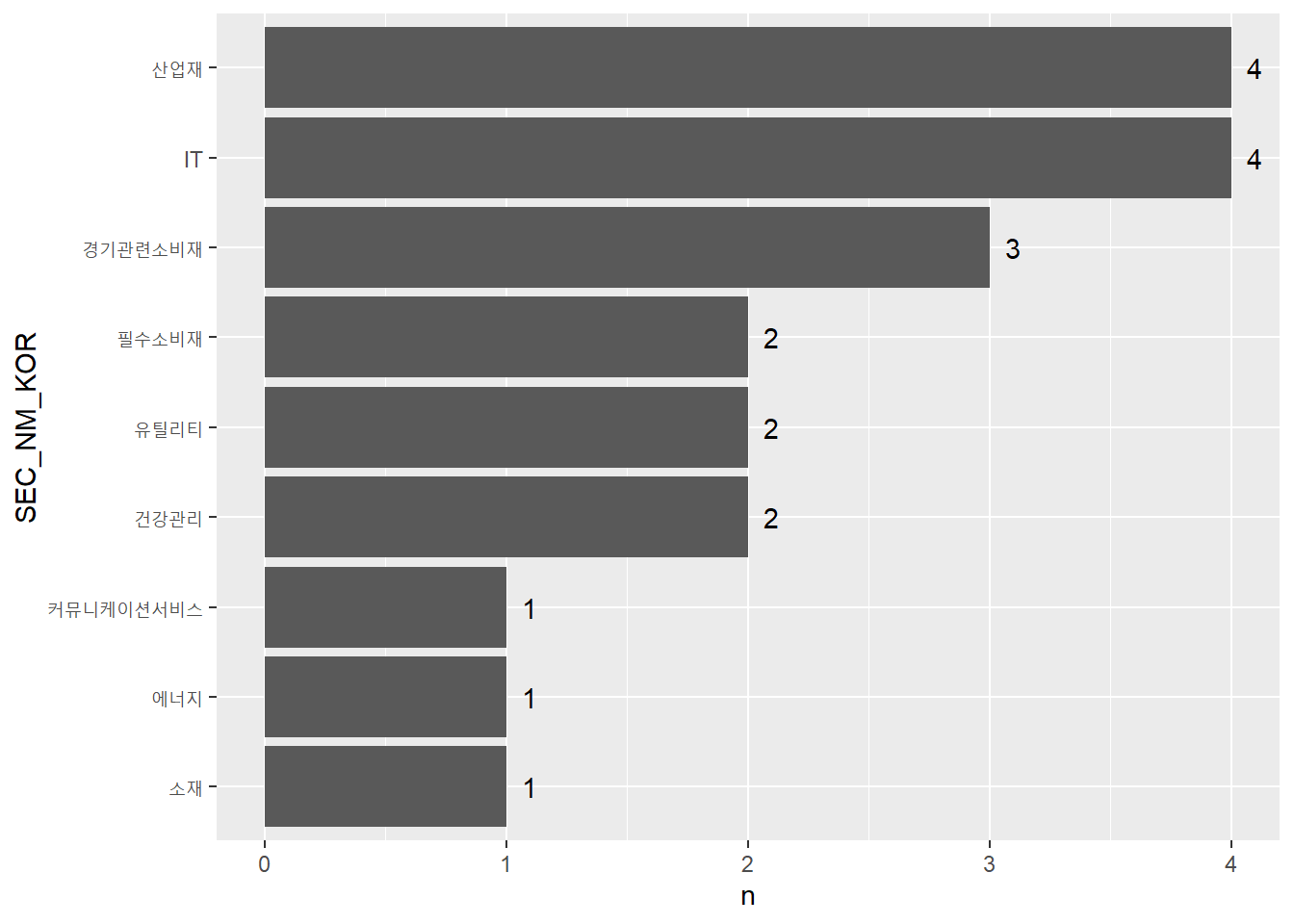
library (DBI)library (RMySQL)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , # 위에서 설정한 root 비밀번호 host = '127.0.0.1' ,dbname = 'stock_db' # 사용하고자 하는 스키마 = dbGetQuery (con,"select * from kor_sector where 기준일 = (select max(기준일) from kor_sector);" = dbGetQuery (con ,"select 날짜, 종가, 종목코드 from kor_price where 날짜 >= (select (select max(날짜) from kor_price) - interval 1 year); " )dbDisconnect (con)= %>% select (날짜, 종목코드, 종가) %>% group_by (종목코드) %>% summarise (ret = last (종가) / first (종가) - 1 )%>% mutate (rank = min_rank (desc (ret))) %>% filter (rank <= 20 ) %>% left_join (sector, by = (c ("종목코드" = "CMP_CD" ))) %>% group_by (SEC_NM_KOR) %>% summarize (n = n ()) %>% arrange (n) %>% mutate (SEC_NM_KOR = factor (SEC_NM_KOR, levels = .$ SEC_NM_KOR %>% unique)) %>% ggplot (aes (x = SEC_NM_KOR, y = n)) + geom_col () + geom_text (aes (label = n, hjust = - 1 )) + coord_flip ()
12개월 기준 모멘텀 상위 종목을 선택한 후, 섹터 테이블을 이용해 섹터별 갯수를 구합니다. 간혹 특정 섹터의 모멘텀이 매우 좋을 경우, 해당 섹터에 쏠림이 심한 경우가 있습니다. 이러한 섹터 쏠림 현상을 제거한 섹터 중립 포트폴리오를 구성해보도록 하겠습니다.
= ret_1yr %>% left_join (sector, by = (c ("종목코드" = "CMP_CD" ))) %>% group_by (SEC_NM_KOR) %>% mutate (scale_per_sector = scale (ret),scale_per_sector = ifelse (is.na (` SEC_NM_KOR ` ),NA , scale_per_sector)) %>% ungroup ()head (ret_1yr_neutral)
# A tibble: 6 × 7
종목코드 ret IDX_CD CMP_KOR SEC_NM_KOR 기준일 scale_per_sector
<chr> <dbl> <chr> <chr> <chr> <chr> <dbl>
1 000020 -0.493 G35 동화약품 건강관리 2022-10-14 -0.572
2 000040 -0.399 G25 KR모터스 경기관련소비재 2022-10-14 -0.342
3 000050 -0.159 G25 경방 경기관련소비재 2022-10-14 0.523
4 000060 0.0549 G40 메리츠화재 금융 2022-10-14 1.82
5 000070 -0.412 G30 삼양홀딩스 필수소비재 2022-10-14 -0.422
6 000080 -0.299 G30 하이트진로 필수소비재 2022-10-14 -0.238
group_by() 함수를 통해 섹터별 그룹을 만들어줍니다.scale() 함수를 이용해 그룹별 정규화를 해줍니다. 정규화는 \(\frac{x-\mu}{\sigma}\) 로 계산됩니다.섹터 정보가 없을 경우 NA로 변경합니다.
위의 정규화 과정을 살펴보면, 전체 종목에서 12개월 수익률을 비교하는 것이 아닌 각 섹터별로 수익률의 강도를 비교하게 됩니다. 따라서 특정 종목의 과거 수익률이 전체 종목과 비교해서 높았더라도 해당 섹터 내에서의 순위가 낮다면, 정규화된 값은 낮아집니다.
따라서 섹터별 정규화 과정을 거친 값으로 비교 분석을 한다면, 섹터 효과가 제거된 포트폴리오를 구성할 수 있습니다.
%>% mutate (rank = min_rank (desc (scale_per_sector))) %>% filter (rank <= 20 )
# A tibble: 20 × 8
종목코드 ret IDX_CD CMP_KOR SEC_NM_KOR 기준일 scale…¹ rank
<chr> <dbl> <chr> <chr> <chr> <chr> <dbl> <int>
1 000230 0.833 G35 일동홀딩스 건강관리 2022-… 3.97 18
2 001570 2.47 G15 금양 소재 2022-… 8.74 3
3 003610 1.38 G25 방림 경기관련소비재 2022-… 6.06 9
4 016790 5.17 G30 카나리아바이오 필수소비재 2022-… 8.68 4
5 025770 1.01 G50 한국정보통신 커뮤니케이션서비… 2022-… 4.90 12
6 030960 2.99 G20 양지사 산업재 2022-… 6.08 8
7 043090 1.13 G25 한창바이오텍 경기관련소비재 2022-… 5.18 11
8 052020 2.02 G45 에스티큐브 IT 2022-… 7.08 5
9 056090 0.939 G35 이노시스 건강관리 2022-… 4.33 16
10 079810 1.04 G45 디이엔티 IT 2022-… 4.02 17
11 095500 2.82 G45 미래나노텍 IT 2022-… 9.60 2
12 101670 6.87 G20 코리아에스이 산업재 2022-… 13.5 1
13 179290 1.58 G35 엠아이텍 건강관리 2022-… 6.52 6
14 205470 0.746 G35 휴마시스 건강관리 2022-… 3.67 19
15 215100 0.707 G25 로보로보 경기관련소비재 2022-… 3.64 20
16 249420 1.05 G35 일동제약 건강관리 2022-… 4.70 13
17 322000 1.49 G10 현대에너지솔루션 에너지 2022-… 4.44 15
18 366030 1.26 G25 공구우먼 경기관련소비재 2022-… 5.64 10
19 373200 1.75 G45 하인크코리아 IT 2022-… 6.26 7
20 376180 0.938 G25 피코그램 경기관련소비재 2022-… 4.48 14
# … with abbreviated variable name ¹scale_per_sector
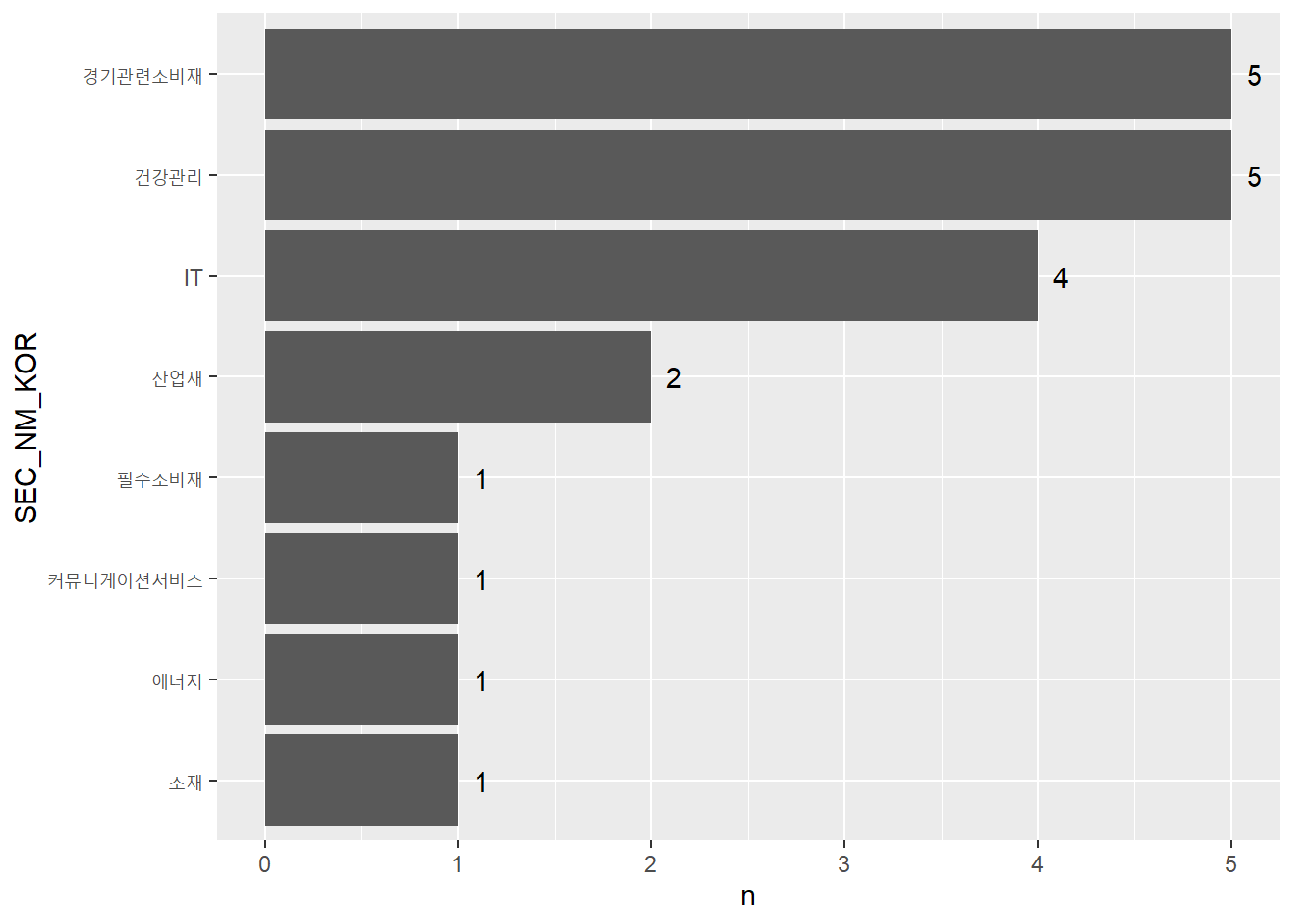
%>% mutate (rank = min_rank (desc (scale_per_sector))) %>% filter (rank <= 20 ) %>% group_by (SEC_NM_KOR) %>% summarize (n = n ()) %>% arrange (n) %>% mutate (SEC_NM_KOR = factor (SEC_NM_KOR, levels = .$ SEC_NM_KOR %>% unique)) %>% ggplot (aes (x = SEC_NM_KOR, y = n)) + geom_col () + geom_text (aes (label = n, hjust = - 1 )) + coord_flip ()
group_by() 함수를 통해 손쉽게 그룹별 중립화를 할 수 있으며, 글로벌 투자를 하는 경우에는 지역, 국가, 섹터별로도 중립화된 포트폴리오를 구성하기도 합니다.
이상치 데이터 처리 및 팩터의 결합
안정적인 퀀트 포트폴리오를 구성하기 위해서는 팩터 데이터를 어떻게 처리하여 결합할지에 대해서도 알고 있어야 하므로, 이러한 점에 대해 살펴보도록 하겠습니다.
모든 데이터 분석에서 중요한 문제 중 하나가 이상치(극단치, Outlier) 데이터를 어떻게 처리할 것인가입니다. 과거 12개월 수익률이 10배인 주식이 과연 모멘텀 관점에서 좋기만 한 주식인지, ROE가 100%를 넘는 주식이 과연 퀄리티 관점에서 좋기만 한 주식인지 고민이 되기 마련입니다. 따라서 이러한 이상치를 제외하고 분석할지, 포함해서 분석할지를 판단해야 합니다. 만일 이상치를 포함한다면 그대로 사용할 것인지, 보정해 사용할 것인지도 판단해야 합니다.
우리가 가지고 있는 PBR 데이터에서 이상치 데이터를 탐색해보도록 하겠습니다.
library (DBI)library (RMySQL)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , host = '127.0.0.1' ,dbname = 'stock_db' = dbGetQuery (con ,"select * from kor_value where 기준일 = (select max(기준일) from kor_value); " )dbDisconnect (con)= value %>% mutate (값 = ifelse (값 <= 0 , NA , 값)) %>% filter (지표 == 'PBR' ) %>% pivot_wider (names_from = '지표' , values_from = '값' ) %>% select (- 기준일)%>% summarize (max_pbr = max (PBR, na.rm = T), min_pbr = min (PBR, na.rm = T))
# A tibble: 1 × 2
max_pbr min_pbr
<dbl> <dbl>
1 40.4 0.0363
먼저 밸류 테이블을 불러온 후 PBR 데이터만 선택합니다. PBR의 최대값과 최소값을 확인해보면 값이 매우 큰 것을 확인할 수 있습니다.
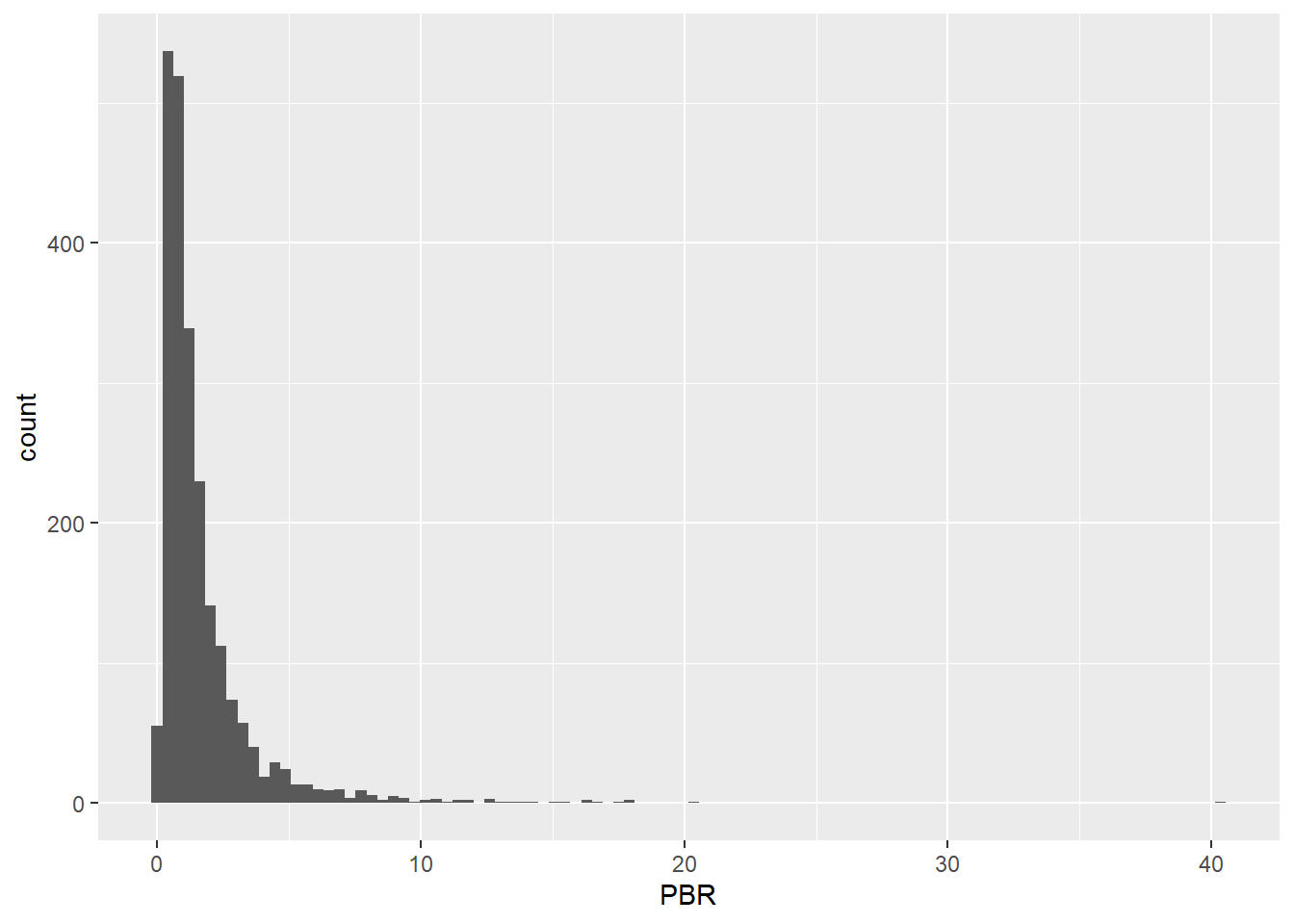
%>% ggplot (aes (x = PBR)) + geom_histogram (bins = 100 )
Warning: Removed 4 rows containing non-finite values (`stat_bin()`).
국내 종목들의 PBR을 히스토그램으로 그려보면 오른쪽으로 꼬리가 매우 긴 분포를 보입니다. 이는 PBR이 극단적으로 큰 이상치 데이터가 있기 때문입니다. 이처럼 모든 팩터 데이터에는 극단치가 있기 마련이며, 이를 처리하는 방법을 알아보도록 하겠습니다.
트림(Trim): 이상치 데이터 삭제
트림은 이상치 데이터를 삭제하는 방법입니다. 위의 예제에서 이상치에 해당하는 상하위 1% 데이터를 삭제하겠습니다.
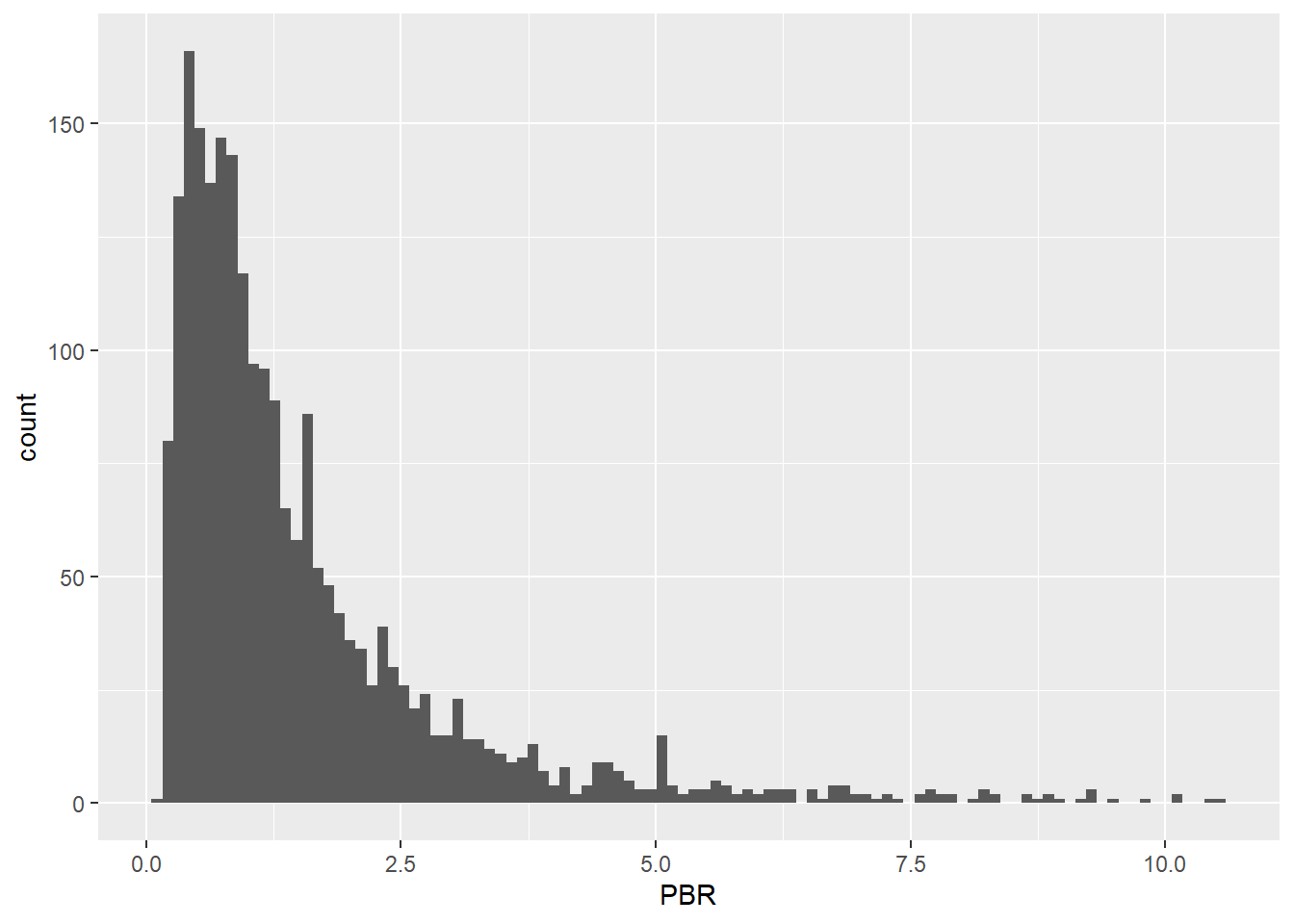
%>% mutate (PBR = ifelse (percent_rank (PBR) > 0.99 , NA , PBR),PBR = ifelse (percent_rank (PBR) < 0.01 , NA , PBR)) %>% ggplot (aes (x = PBR)) + geom_histogram (bins = 100 )
Warning: Removed 50 rows containing non-finite values (`stat_bin()`).
percent_rank() 함수를 통해 백분위를 구한 후 상하위 1%에 해당하는 데이터를 제외한 데이터만 선택합니다. 결과적으로 지나치게 PBR이 낮은 종목과 높은 종목은 제거되어 \(x\) 축의 스케일이 많이 줄어든 모습입니다.
평균이나 분산 같이 통계값을 구하는 과정에서는 이상치 데이터를 제거하는 것이 바람직할 수 있습니다. 그러나 팩터를 이용해 포트폴리오를 구하는 과정에서 해당 방법은 조심스럽게 사용되어야 합니다. 데이터의 손실이 발생하게 되며, 제거된 종목 중 정말로 좋은 종목이 있을 수도 있기 때문입니다.
윈저라이징(Winsorizing): 이상치 데이터 대체
이상치 데이터를 다른 데이터로 대체하는 윈저라이징 방법을 사용할 수도 있습니다. 예를 들어 상위 1%를 초과하는 데이터는 1% 값으로 대체하며, 하위 1% 미만의 데이터는 1% 데이터로 대체합니다. 즉, 좌우로 울타리를 쳐놓고 해당 범위를 넘어가는 값을 강제로 울타리에 맞춰줍니다.
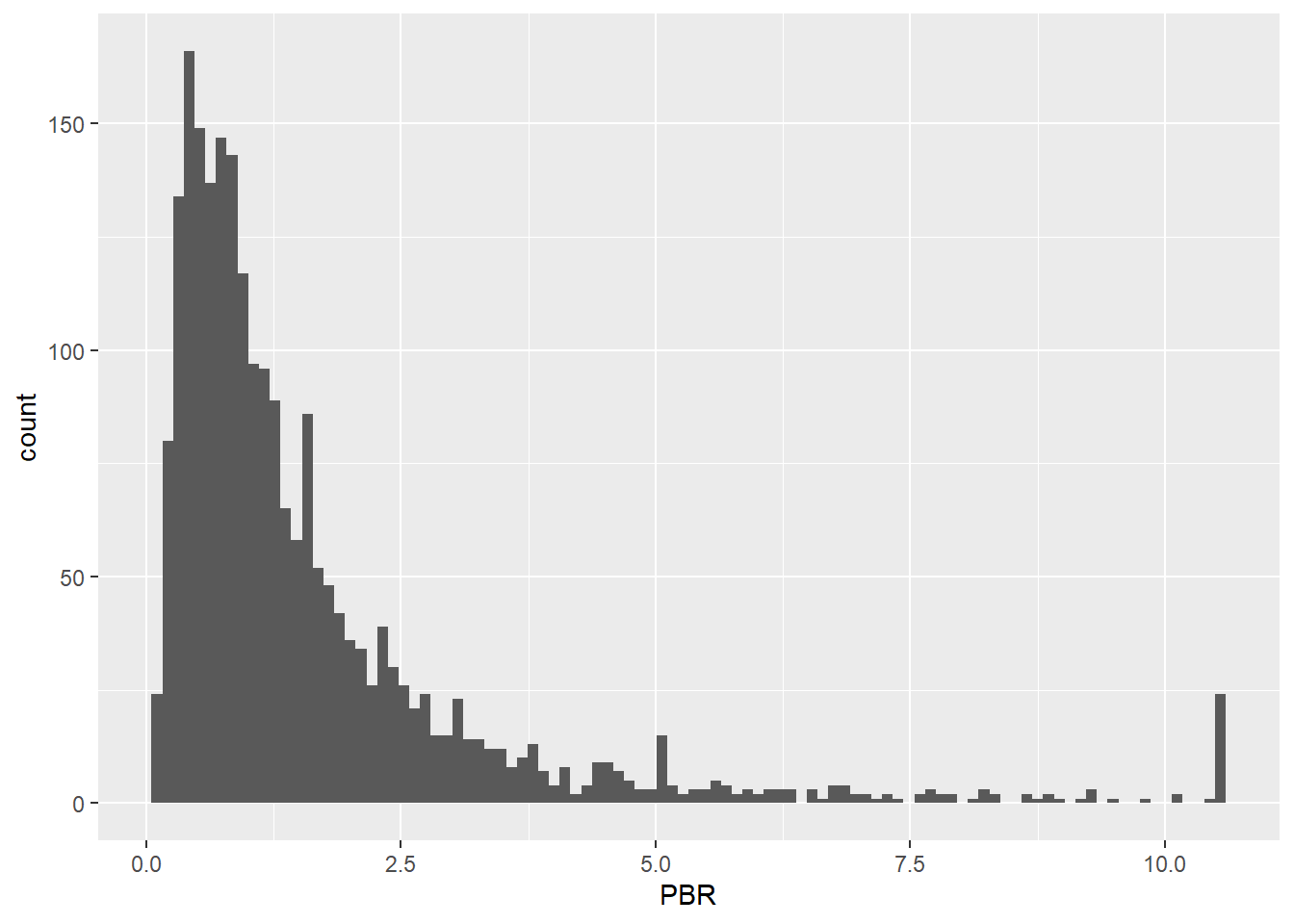
%>% mutate (PBR = ifelse (percent_rank (PBR) > 0.99 ,quantile (.$ PBR, 0.99 , na.rm = TRUE ), PBR),PBR = ifelse (percent_rank (PBR) < 0.01 ,quantile (.$ PBR, 0.01 , na.rm = TRUE ), PBR)) %>% ggplot (aes (x = PBR)) + geom_histogram (bins = 100 )
Warning: Removed 4 rows containing non-finite values (`stat_bin()`).
이번에는 값이 상하위 1%를 벗어나는 경우, 1%에 해당하는 값으로 대체하였습니다. 그림을 살펴보면 축 양 끝부분의 막대(붉은색)가 길어진 것을 확인할 수 있습니다.
팩터의 결합방법
앞서 밸류 지표의 결합, 퀄리티 지표의 결합, 마법공식 포트폴리오를 구성할 때는 단순히 순위를 더하는 방법을 사용했습니다. 물론 투자 종목수가 얼마 되지 않거나, 개인 투자자의 입장에서는 이러한 방법이 가장 단순하면서도 효과적일수 있습니다. 그러나 전문투자자가 포트폴리오를 구성하거나 팩터를 분석하는 업무를 할 경우 이처럼 단순히 순위를 더하는 방법은 여러 가지 문제를 안고 있습니다.
각 밸류 지표의 순위를 구한 후 히스토그램으로 나타내보도록 하겠습니다.
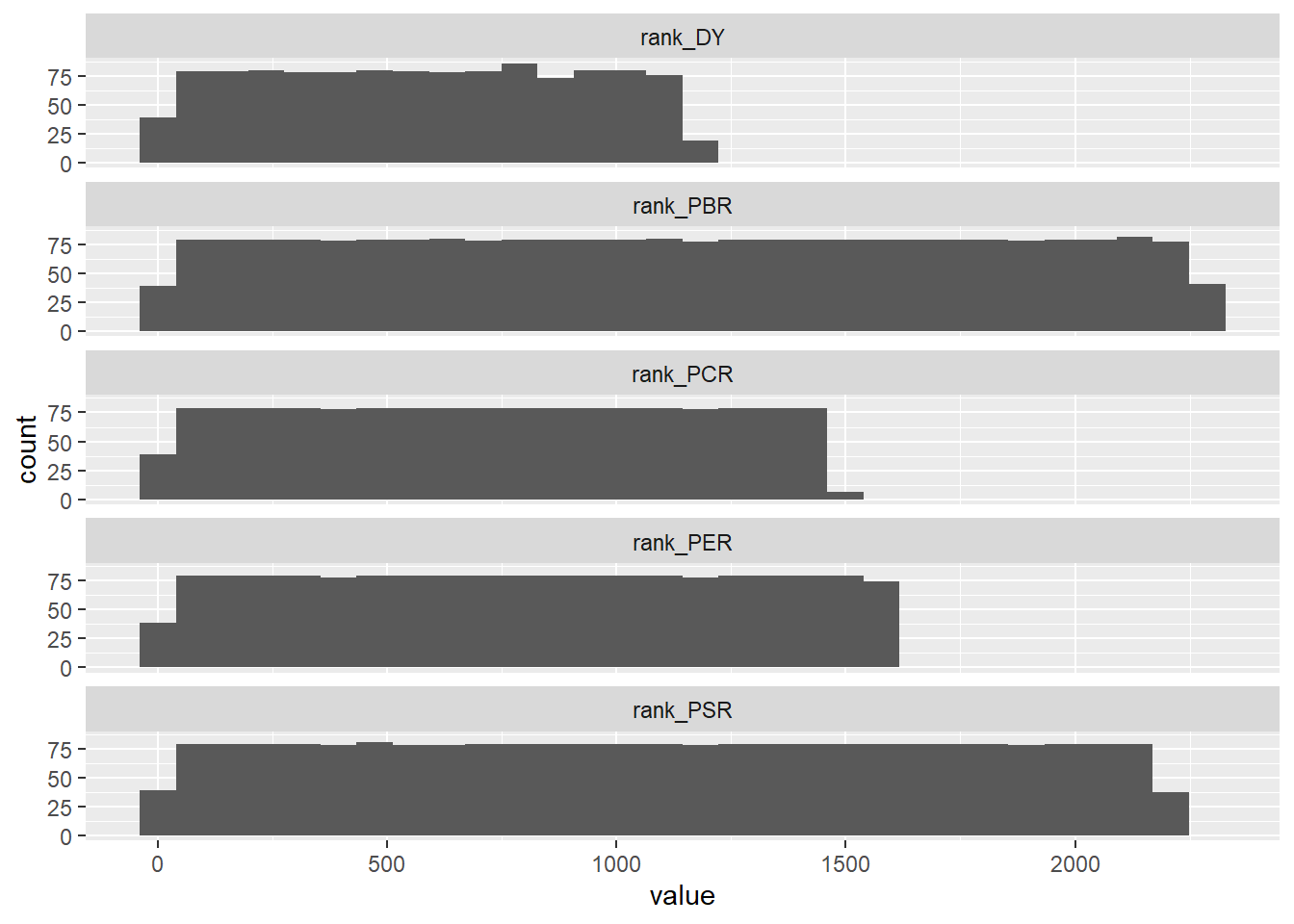
library (DBI)library (RMySQL)= dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , # 위에서 설정한 root 비밀번호 host = '127.0.0.1' ,dbname = 'stock_db' # 사용하고자 하는 스키마 = dbGetQuery (con,"select * from kor_ticker where 기준일 = (select max(기준일) from kor_ticker) and 종목구분 = '보통주';" )= dbGetQuery (con ,"select * from kor_value where 기준일 = (select max(기준일) from kor_value); " )dbDisconnect (con)= value %>% mutate (값 = ifelse (값 <= 0 , NA , 값)) %>% pivot_wider (names_from = '지표' , values_from = '값' ) %>% select (- 기준일) %>% mutate (across (c (PBR, PER, PCR, PSR), min_rank, .names = "rank_{col}" )) %>% mutate (rank_DY = min_rank (desc (DY)))%>% select (종목코드, contains ('rank_' )) %>% pivot_longer (- 종목코드) %>% ggplot (aes (x = value)) + geom_histogram () + facet_wrap (name ~ . , ncol = 1 )
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2729 rows containing non-finite values (`stat_bin()`).
그림에서 알 수 있듯이 순위를 구하는 것의 가장 큰 장점은 극단치로 인한 효과가 사라진다는 점과 균등한 분포를 가진다는 점입니다. 그러나 각 지표의 \(x\) 축을 보면 최댓값이 서로 다릅니다. 이는 지표별 결측치로 인해 유효 데이터의 갯수가 달라 나타나는 현상입니다.
%>% select (종목코드, contains ('rank_' )) %>% pivot_longer (- 종목코드) %>% group_by (name) %>% summarize (na_count = sum (is.na (value)))
# A tibble: 5 × 2
name na_count
<chr> <int>
1 rank_DY 1130
2 rank_PBR 4
3 rank_PCR 828
4 rank_PER 681
5 rank_PSR 86
밸류 지표 별 NA 개수를 확인해보면 그 결과가 모두 다르며, 특히 배당 수익률의 경우 절반 정도가 NA 데이터입니다. 따라서 서로 다른 범위의 분포를 단순히 합치는 것은 좋은 방법이 아닙니다. 예를 들어 A, B, C, D 팩터에 각각 비중을 25%, 25%, 25%, 25% 부여해 포트폴리오를 구성한다고 가정해봅시다. 각 순위는 분포의 범위가 다르므로, 순위와 비중의 가중평균을 통해 포트폴리오를 구성하면 왜곡된 결과를 발생시킵니다.
이러한 문제를 해결하는 가장 좋은 방법은 순위를 구한 후 이를 Z-Score로 정규화하는 것입니다.
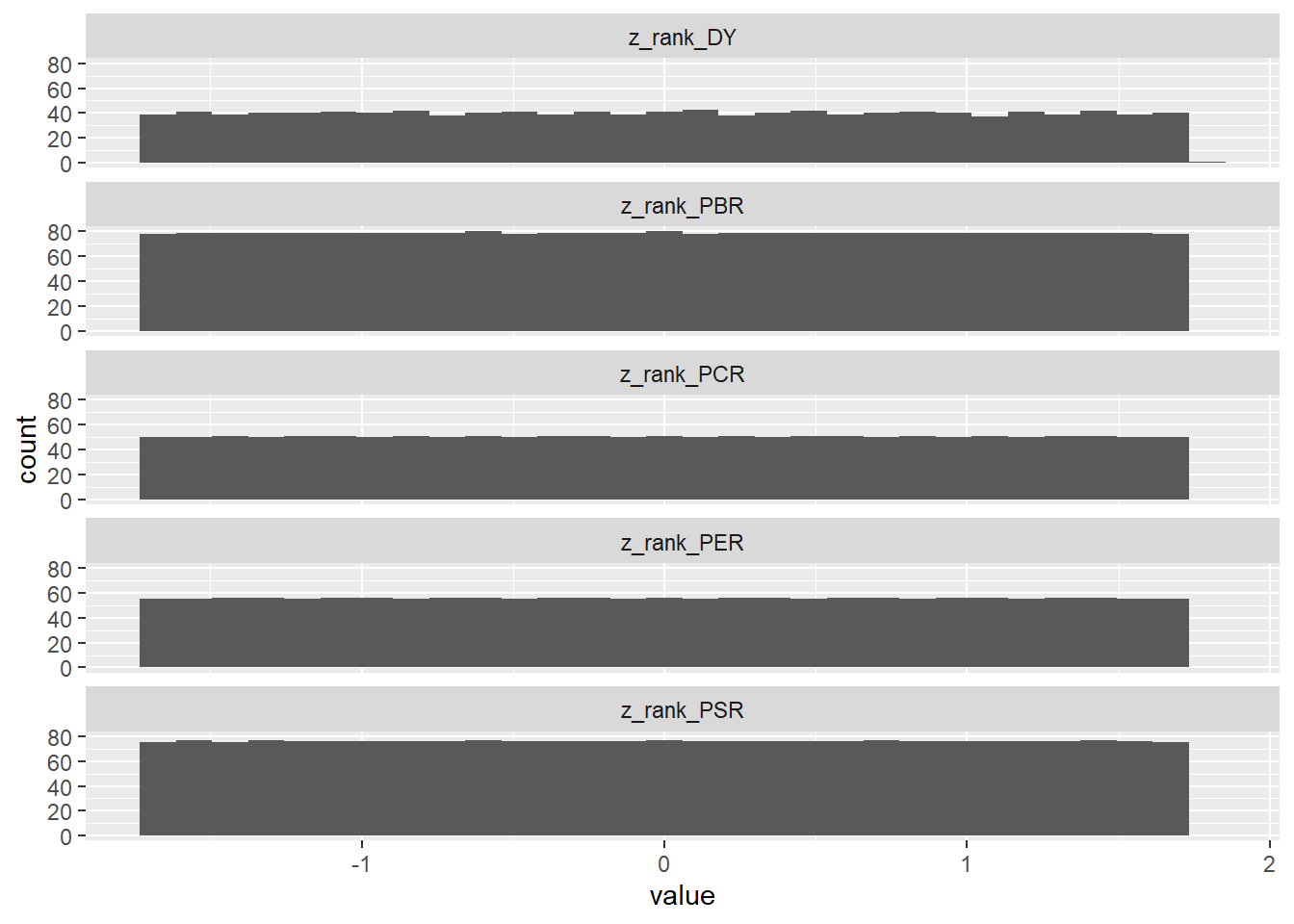
= value %>% select (1 : 6 ) %>% mutate (across (c (PBR, PER, PCR, PSR), min_rank, .names = "rank_{col}" )) %>% mutate (rank_DY = min_rank (desc (DY))) %>% mutate (across (c (rank_PBR, rank_PER, rank_PCR, rank_PSR, rank_DY), scale, .names = "z_{col}" )) %>% select (종목코드, contains ('z_' )) %>% pivot_longer (- 종목코드) %>% ggplot (aes (x = value)) + geom_histogram () + facet_wrap (name ~ . , ncol = 1 )
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2729 rows containing non-finite values (`stat_bin()`).
앞서 구해진 순위에 scale 함수를 통해 정규화를 해줍니다. 기본적으로 순위의 분포가 가진 극단치 효과가 사라지는 점과 균등 분포의 장점을 유지하고 있으며, 분포의 범위 역시 거의 동일하게 바뀌었습니다. 이처럼 여러 팩터를 결합해 포트폴리오를 구성하고자 하는 경우, 먼저 각 팩터(지표)별 순위를 구한 후 이를 정규화한 뒤 더해야 왜곡 효과가 제거되어 안정적인 포트폴리오가 됩니다.
\[Z-Score(Rank(Factor\ A)) + Z-Score(Rank(Factor\ B)) + \dots + Z-Score(Rank(Factor\ N))\]
멀티팩터 포트폴리오
앞에서 배웠던 팩터 이론들과 결합 방법들을 응용해 멀티팩터 포트폴리오를 구성해봅시다. 각 팩터에 사용되는 지표는 다음과 같습니다.
퀄리티: 자기자본이익률(ROE), 매출총이익(GPA), 영업활동현금흐름(CFO)
밸류: PER, PBR, PSR, PCR, DY
모멘텀: 12개월 수익률, K-Ratio
library (DBI)library (RMySQL)# 연결 = dbConnect (drv = MySQL (),user = 'root' ,password = '1234' , host = '127.0.0.1' ,dbname = 'stock_db' # 티커 = dbGetQuery (con,"select * from kor_ticker where 기준일 = (select max(기준일) from kor_ticker) and 종목구분 = '보통주';" )# 주가 = dbGetQuery (con ,"select 날짜, 종가, 종목코드 from kor_price where 날짜 >= (select (select max(날짜) from kor_price) - interval 1 year); " )# 밸류 = dbGetQuery (con ,"select * from kor_value where 기준일 = (select max(기준일) from kor_value); " )# 재무제표 = dbGetQuery (con ,"select * from kor_fs where 계정 in ('당기순이익', '매출총이익', '영업활동으로인한현금흐름', '자산', '자본') and 공시구분 = 'q'; " )# 섹터 = dbGetQuery (con,"select * from kor_sector where 기준일 = (select max(기준일) from kor_sector);" dbDisconnect (con)
티커, 섹터, 주가, 재무제표, 가치지표 데이터를 불러옵니다.
= value %>% mutate (값 = ifelse (값 <= 0 , NA , 값)) %>% pivot_wider (names_from = '지표' , values_from = '값' ) %>% select (- 기준일) %>% mutate (across (c (PBR, PER, PCR, PSR), min_rank, .names = "rank_{col}" )) %>% mutate (rank_DY = min_rank (desc (DY)))
가치지표를 핸들링합니다.
library (RcppRoll)= fs %>% arrange (종목코드, 계정, 기준일) %>% group_by (종목코드, 계정) %>% mutate (rollsum = roll_sum (값, n = 4 , align = 'right' , fill = NA )) %>% slice (n ()) %>% mutate (rollsum = case_when (%in% c ('자본' , '자산' ) ~ rollsum / 4 ,TRUE ~ rollsum%>% ungroup ()= fs_roll %>% select (계정, 종목코드, rollsum) %>% pivot_wider (names_from = 계정, values_from = rollsum) %>% mutate (ROE = 당기순이익 / 자본,GPA = 매출총이익 / 자산,CFO = 영업활동으로인한현금흐름 / 자산)
퀄리티 지표를 계산하기 위해 TTM 기준 ROE, GPA, CFO를 계산합니다.
= %>% select (날짜, 종목코드, 종가) %>% group_by (종목코드) %>% slice_tail (n = 255 ) %>% summarise (ret = last (종가) / first (종가) - 1 )= price %>% group_by (종목코드) %>% filter (n () >= 200 ) %>% mutate (ret = 종가 / lag (종가) - 1 ) %>% mutate (ret = log (1 + ret)) %>% slice (- 1 ) %>% mutate (cumret = cumsum (ret)) %>% mutate (id = row_number ()) %>% ungroup () %>% nest (data = - 종목코드) %>% mutate (model = map (data, ~ lm (cumret~ id, data = .)),tidied = map (model, tidy)) %>% unnest (tidied) %>% filter (term == 'id' ) %>% mutate (k_ratio = estimate / ` std.error ` )
최근 12개월 수익률과 K-Ratio를 계산합니다. 이제 모든 테이블을 하나로 합치도록 합니다.
library (tibble)= %>% left_join (sector, by = c ('종목코드' = 'CMP_CD' )) %>% left_join (fs_roll_pivot %>% select (종목코드, ROE, GPA, CFO)) %>% left_join (value) %>% left_join (ret_1yr) %>% left_join (k_ratio %>% select (종목코드, k_ratio))
Joining, by = "종목코드"
Joining, by = "종목코드"
Joining, by = "종목코드"
Joining, by = "종목코드"
= data_bind %>% mutate (SEC_NM_KOR = replace_na (SEC_NM_KOR, '기타' )) %>% as_tibble ()
# A tibble: 2,294 × 30
종목코드 종목명 시장…¹ 종가 시가총액 기준…² EPS 선행EPS BPS 주당…³
<chr> <chr> <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 000020 동화약품 KOSPI 8650 2.42e11 2022-1… 647 NA 12534 180
2 000040 KR모터스 KOSPI 599 5.76e10 2022-1… NA NA 385 0
3 000050 경방 KOSPI 10800 2.96e11 2022-1… 872 NA 30033 125
4 000060 메리츠화… KOSPI 29600 3.37e12 2022-1… 5768 6808 22086 620
5 000070 삼양홀딩… KOSPI 63800 5.46e11 2022-1… 30711 NA 226314 3000
6 000080 하이트진… KOSPI 24650 1.73e12 2022-1… 1031 1984 15657 800
7 000100 유한양행 KOSPI 55000 4.03e12 2022-1… 1496 1673 28297 400
8 000120 CJ대한통… KOSPI 81000 1.85e12 2022-1… 1841 10250 178766 0
9 000140 하이트진… KOSPI 10050 2.33e11 2022-1… 1529 NA 23538 450
10 000150 두산 KOSPI 78600 1.30e12 2022-1… 11890 12800 121631 2000
# … with 2,284 more rows, 20 more variables: 종목구분 <chr>, IDX_CD <chr>,
# CMP_KOR <chr>, SEC_NM_KOR <chr>, 기준일.y <chr>, ROE <dbl>, GPA <dbl>,
# CFO <dbl>, DY <dbl>, PBR <dbl>, PCR <dbl>, PER <dbl>, PSR <dbl>,
# rank_PBR <int>, rank_PER <int>, rank_PCR <int>, rank_PSR <int>,
# rank_DY <int>, ret <dbl>, k_ratio <dbl>, and abbreviated variable names
# ¹시장구분, ²기준일.x, ³주당배당금
테이블을 합친 후, 섹터 정보가 없는 경우 ’기타’를 입력합니다.
이번에는 각 섹터별로 아웃라이어를 제거한 후 순위와 Z-Score를 구하도록 하겠습니다. 첫번째로 퀄리티 지표의 Z-Score를 계산합니다.
= data_bind %>% select (종목코드, SEC_NM_KOR, ROE, GPA, CFO) %>% group_by (SEC_NM_KOR) %>% mutate (across (c (ROE, GPA, CFO), .fns = ~ min_rank (desc (.)), .names = "rank_{col}" )) %>% mutate (across (c (rank_ROE, rank_GPA, rank_CFO), .fns = ~ scale (.), .names = "z_{col}" )) %>% mutate (z_quality = rowSums (across (contains ('z_rank' )))) %>% ungroup ()= data_bind %>% left_join (z_quality %>% select (종목코드, z_quality))
# A tibble: 2,294 × 31
종목코드 종목명 시장…¹ 종가 시가총액 기준…² EPS 선행EPS BPS 주당…³
<chr> <chr> <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 000020 동화약품 KOSPI 8650 2.42e11 2022-1… 647 NA 12534 180
2 000040 KR모터스 KOSPI 599 5.76e10 2022-1… NA NA 385 0
3 000050 경방 KOSPI 10800 2.96e11 2022-1… 872 NA 30033 125
4 000060 메리츠화… KOSPI 29600 3.37e12 2022-1… 5768 6808 22086 620
5 000070 삼양홀딩… KOSPI 63800 5.46e11 2022-1… 30711 NA 226314 3000
6 000080 하이트진… KOSPI 24650 1.73e12 2022-1… 1031 1984 15657 800
7 000100 유한양행 KOSPI 55000 4.03e12 2022-1… 1496 1673 28297 400
8 000120 CJ대한통… KOSPI 81000 1.85e12 2022-1… 1841 10250 178766 0
9 000140 하이트진… KOSPI 10050 2.33e11 2022-1… 1529 NA 23538 450
10 000150 두산 KOSPI 78600 1.30e12 2022-1… 11890 12800 121631 2000
# … with 2,284 more rows, 21 more variables: 종목구분 <chr>, IDX_CD <chr>,
# CMP_KOR <chr>, SEC_NM_KOR <chr>, 기준일.y <chr>, ROE <dbl>, GPA <dbl>,
# CFO <dbl>, DY <dbl>, PBR <dbl>, PCR <dbl>, PER <dbl>, PSR <dbl>,
# rank_PBR <int>, rank_PER <int>, rank_PCR <int>, rank_PSR <int>,
# rank_DY <int>, ret <dbl>, k_ratio <dbl>, z_quality <dbl>, and abbreviated
# variable names ¹시장구분, ²기준일.x, ³주당배당금
두번째로 밸류 지표의 Z-Score를 계산합니다.
= %>% select (종목코드, SEC_NM_KOR, DY, PBR, PCR, PER, PSR) %>% group_by (SEC_NM_KOR) %>% mutate (rank_DY = min_rank (desc (DY))) %>% mutate (across (c (PBR, PCR, PER, PSR), .fns = ~ min_rank (.), .names = "rank_{col}" )) %>% mutate (across (c (rank_DY, rank_PBR, rank_PCR, rank_PER, rank_PSR), .fns = ~ scale (.), .names = "z_{col}" )) %>% mutate (z_value = rowSums (across (contains ('z_rank' )))) %>% ungroup ()= data_bind %>% left_join (z_value %>% select (종목코드, z_value))
마지막으로 모멘텀 지표의 Z-Score를 구합니다.
= %>% select (종목코드, SEC_NM_KOR, ret, k_ratio) %>% group_by (SEC_NM_KOR) %>% mutate (across (c (ret, k_ratio), .fns = ~ min_rank (desc (.)), .names = "rank_{col}" )) %>% mutate (across (c (rank_ret, rank_k_ratio), .fns = ~ scale (.), .names = "z_{col}" )) %>% mutate (z_momentum = rowSums (across (contains ('z_rank' )))) %>% ungroup ()= data_bind %>% left_join (z_momentum %>% select (종목코드, z_momentum))
각 팩터의 분포를 시각화해보도록 하겠습니다.
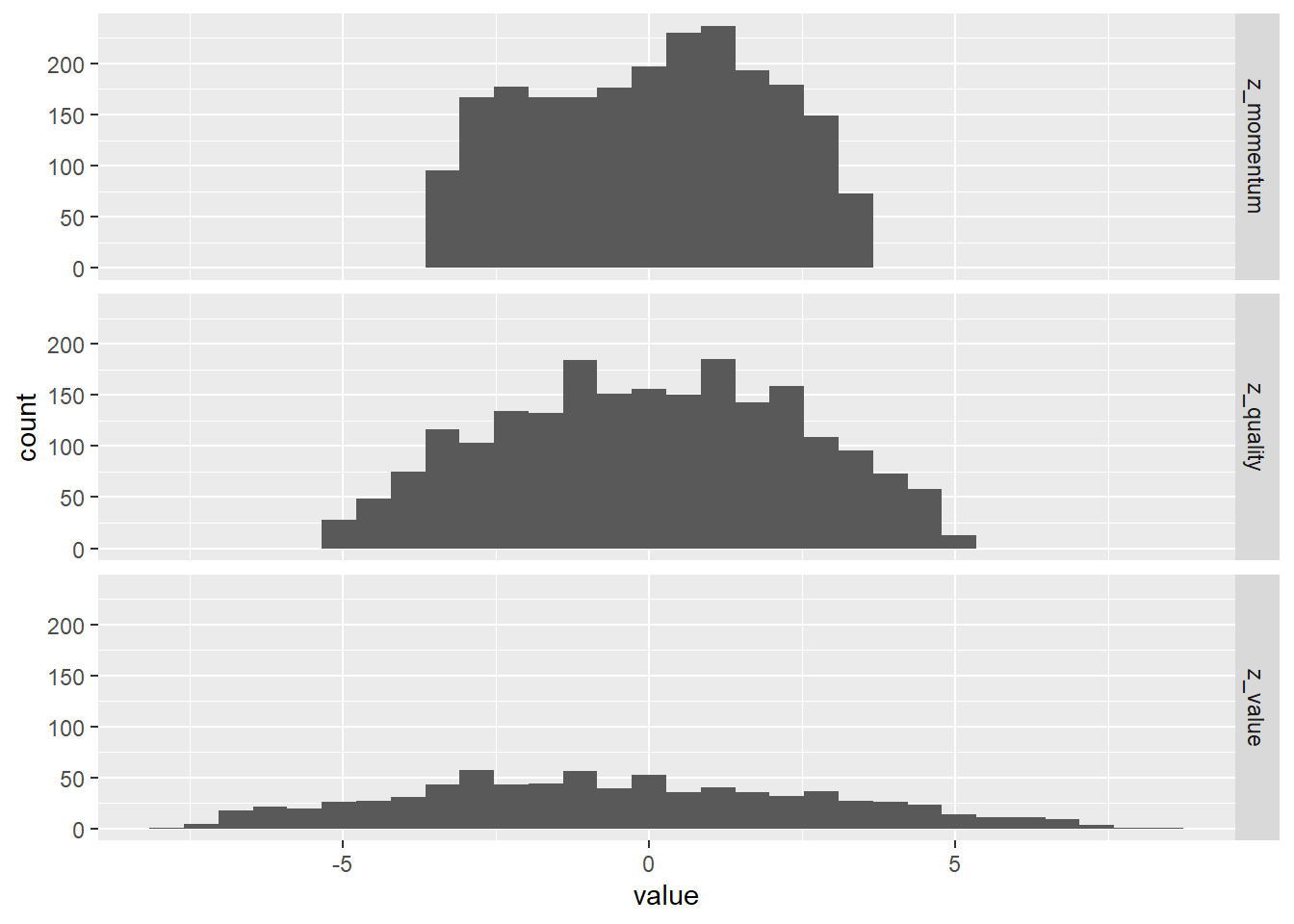
%>% select (종목코드, contains ('z_' )) %>% pivot_longer (- 종목코드) %>% ggplot (aes (x = value)) + geom_histogram () + facet_grid (name ~ .)
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 1768 rows containing non-finite values (`stat_bin()`).
각각 퀄리티 지표는 3개, 밸류 지표는 5개, 모멘텀 지표는 2개 기준을 이용해 계산했습니다. 그림에서 알 수 있듯이 기준을 많이 사용할 수록 Z-Score가 넓게 퍼져있는 모습을 보이며, 각 팩터별 분포가 동일하지 않습니다. 따라서 다시 Z-Score를 계산해 분포의 넓이를 비슷하게 맞춰주도록 합니다.
Attaching package: 'magrittr'
The following object is masked from 'package:purrr':
set_names
The following object is masked from 'package:tidyr':
extract
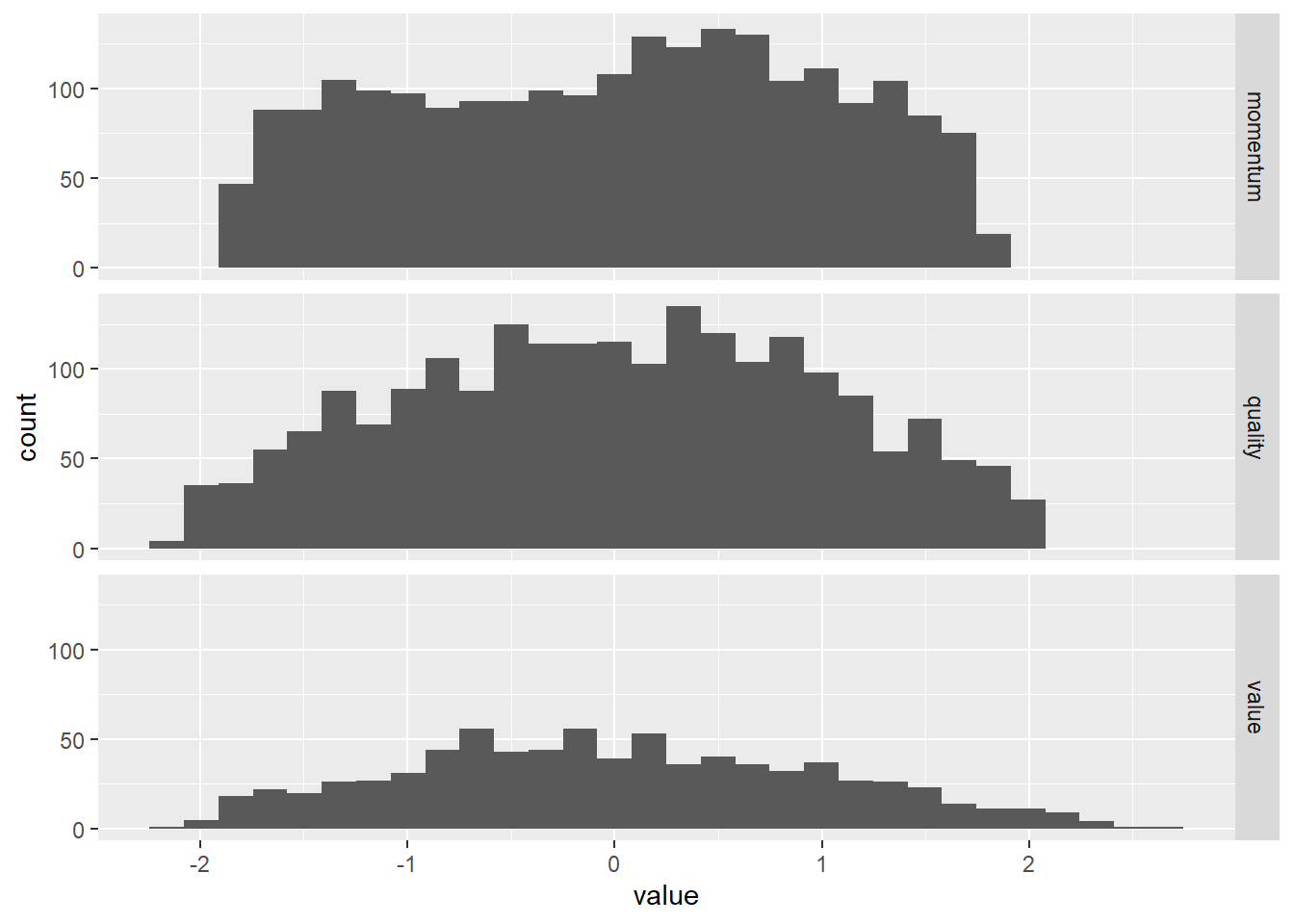
= data_bind %>% select (종목코드, z_quality, z_value, z_momentum) %>% mutate (across (c (z_quality, z_value, z_momentum), .fns = ~ scale (.))) %>% set_colnames (c ('종목코드' , 'quality' , 'value' , 'momentum' ))%>% pivot_longer (- 종목코드) %>% ggplot (aes (x = value)) + geom_histogram () + facet_grid (name ~ .)
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 1768 rows containing non-finite values (`stat_bin()`).
재계산된 Z-Score의 분포의 넓이를 살펴보면 이전에 비해 훨씬 비슷해진 것을 알 수 있습니다. 각 팩터들 간의 상관관계를 살펴보겠습니다.
%>% select (- 종목코드) %>% cor (., use = 'complete.obs' ) %>% round (., 2 )
quality value momentum
quality 1.00 0.08 0.08
value 0.08 1.00 -0.15
momentum 0.08 -0.15 1.00
각 팩터간 상관관계가 매우 낮으며, 여러 팩터를 동시에 고려함으로서 분산효과를 기대할 수 있습니다. 이제 계산된 팩터들을 토대로 최종 포트폴리오를 구성해보도록 하겠습니다.
= c (0.3 , 0.3 , 0.3 )= data_bind_final %>% column_to_rownames ('종목코드' ) %>% multiply_by (wts) %>% mutate (qvm = rowSums (.)) %>% rownames_to_column (var = '종목코드' ) %>% select (종목코드, qvm)= data_bind %>% left_join (data_bind_final) %>% mutate (invest = ifelse (min_rank (qvm) <= 20 , 'Y' , 'N' ))%>% filter (invest == 'Y' )
# A tibble: 20 × 35
종목코드 종목명 시장…¹ 종가 시가총액 기준…² EPS 선행EPS BPS 주당…³
<chr> <chr> <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 000700 유수홀… KOSPI 6350 1.65e11 2022-1… 991 NA 13108 400
2 001120 LX인터… KOSPI 42750 1.66e12 2022-1… 9733 11746 49349 2300
3 005010 휴스틸 KOSPI 5810 2.28e11 2022-1… 987 NA 15984 160
4 009970 영원무… KOSPI 51200 6.98e11 2022-1… 19026 22866 140307 2000
5 017670 SK텔레콤 KOSPI 49700 1.09e13 2022-1… 7191 5167 53218 3295
6 030200 KT KOSPI 34800 9.09e12 2022-1… 5759 5188 63512 1910
7 036710 심텍홀… KOSDAQ 3140 1.52e11 2022-1… 695 NA 4051 50
8 049070 인탑스 KOSDAQ 27800 4.78e11 2022-1… 4436 4244 32446 470
9 058860 KTis KOSPI 2430 8.46e10 2022-1… 767 NA 5909 100
10 065510 휴비츠 KOSDAQ 10000 1.19e11 2022-1… 848 2383 8297 200
11 078930 GS KOSPI 45950 4.27e12 2022-1… 15304 19446 108672 2000
12 084650 랩지노… KOSDAQ 7110 2.42e11 2022-1… 2497 NA 4747 300
13 093050 LF KOSPI 15450 4.52e11 2022-1… 4169 NA 46904 600
14 094970 제이엠티 KOSDAQ 3115 5.22e10 2022-1… 908 NA 4505 150
15 124560 태웅로… KOSDAQ 4805 1.85e11 2022-1… 1726 NA 3292 100
16 200880 서연이화 KOSPI 6630 1.79e11 2022-1… 973 NA 24588 150
17 205470 휴마시스 KOSDAQ 17850 6.11e11 2022-1… 4422 NA 5908 200
18 225220 제놀루션 KOSDAQ 9700 9.30e10 2022-1… 3626 NA 9083 400
19 306200 세아제강 KOSPI 142000 4.03e11 2022-1… 32640 64527 242703 3500
20 319660 피에스… KOSDAQ 17150 2.48e11 2022-1… 2615 2896 9888 600
# … with 25 more variables: 종목구분 <chr>, IDX_CD <chr>, CMP_KOR <chr>,
# SEC_NM_KOR <chr>, 기준일.y <chr>, ROE <dbl>, GPA <dbl>, CFO <dbl>,
# DY <dbl>, PBR <dbl>, PCR <dbl>, PER <dbl>, PSR <dbl>, rank_PBR <int>,
# rank_PER <int>, rank_PCR <int>, rank_PSR <int>, rank_DY <int>, ret <dbl>,
# k_ratio <dbl>, z_quality <dbl>, z_value <dbl>, z_momentum <dbl>, qvm <dbl>,
# invest <chr>, and abbreviated variable names ¹시장구분, ²기준일.x,
# ³주당배당금
각 팩터별 비중을 리스트로 만들며, 0.3으로 동일한 비중을 입력합니다다. 비중을 [0.2, 0.4, 0.4]와 같이 팩터별로 다르게 줄 수도 있으며, 이는 어떠한 팩터를 더욱 중요하게 생각하는지 혹은 더욱 좋게 보는지에 따라 조정이 가능합니다.
팩터별 Z-Score와 비중의 곱을 구한 후 이를 합합니다.
기존 테이블(data_bind)과 합칩니다.
최종 Z-Score의 합(qvm) 기준 순위가 1~20인 경우는 투자 종목에 해당하므로 ‘Y’, 그렇지 않으면 ’N’으로 표시합니다.
최종 선택된 종목들을 보면 전반적으로 퀄리티가 높고, 밸류에이션이 낮으며, 최근 수익률이 높습니다. 물론 특정 팩터(예: 모멘텀)가 좋지 않아도 다른 팩터(예: 밸류)가 지나치게 좋아 선택되는 경우도 있습니다. 이제 선택된 종목들과 그렇지 않은 종목들간의 특성을 그림으로 표현해보겠습니다.
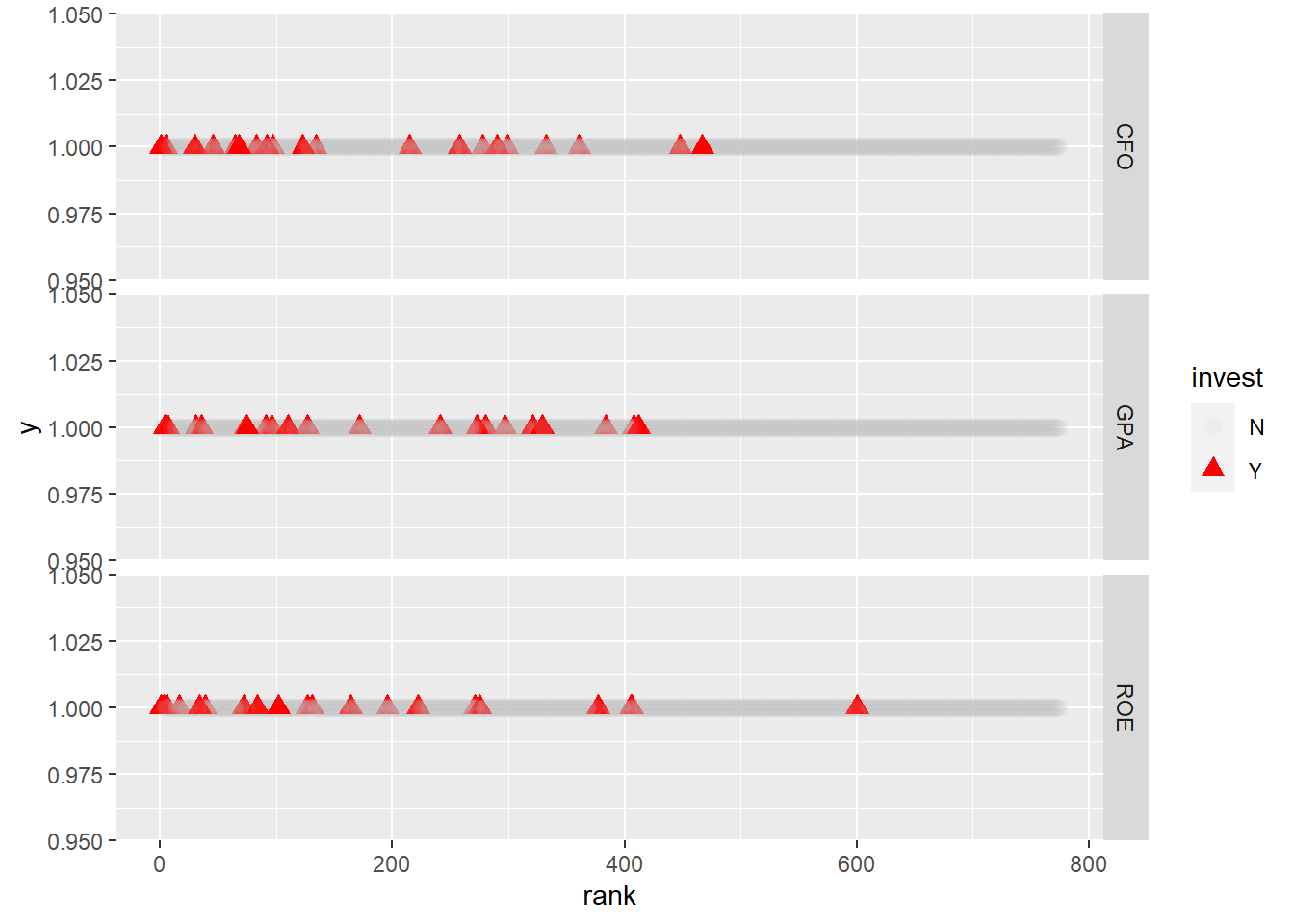
%>% select (ROE, GPA, CFO, invest) %>% na.omit () %>% pivot_longer (- invest) %>% group_by (name) %>% mutate (rank = min_rank (desc (value))) %>% ggplot (aes (x = rank, y = 1 , shape = invest, color = invest, alpha = invest)) + geom_point (size = 3 ) + scale_color_manual (values= c ("grey" , "red" )) + facet_grid (name~ .)
Warning: Using alpha for a discrete variable is not advised.
퀄리티 지표가 포함된 데이터를 선택한다.
각 지표(name)별 그룹을 묶은 후 순위를 계산합니다.
그림으로 나타냅니다.
붉은색 ▲ 마크는 투자하는 종목, 회색 ● 마크는 투자하지 않는 종목입니다. 전반적으로 멀티팩터 기준으로 선정된 종목들의 퀄리티 순위가 높음을 알 수 있습니다.
이번에는 동일한 방법으로 밸류 지표의 차이를 살펴보겠습니다.
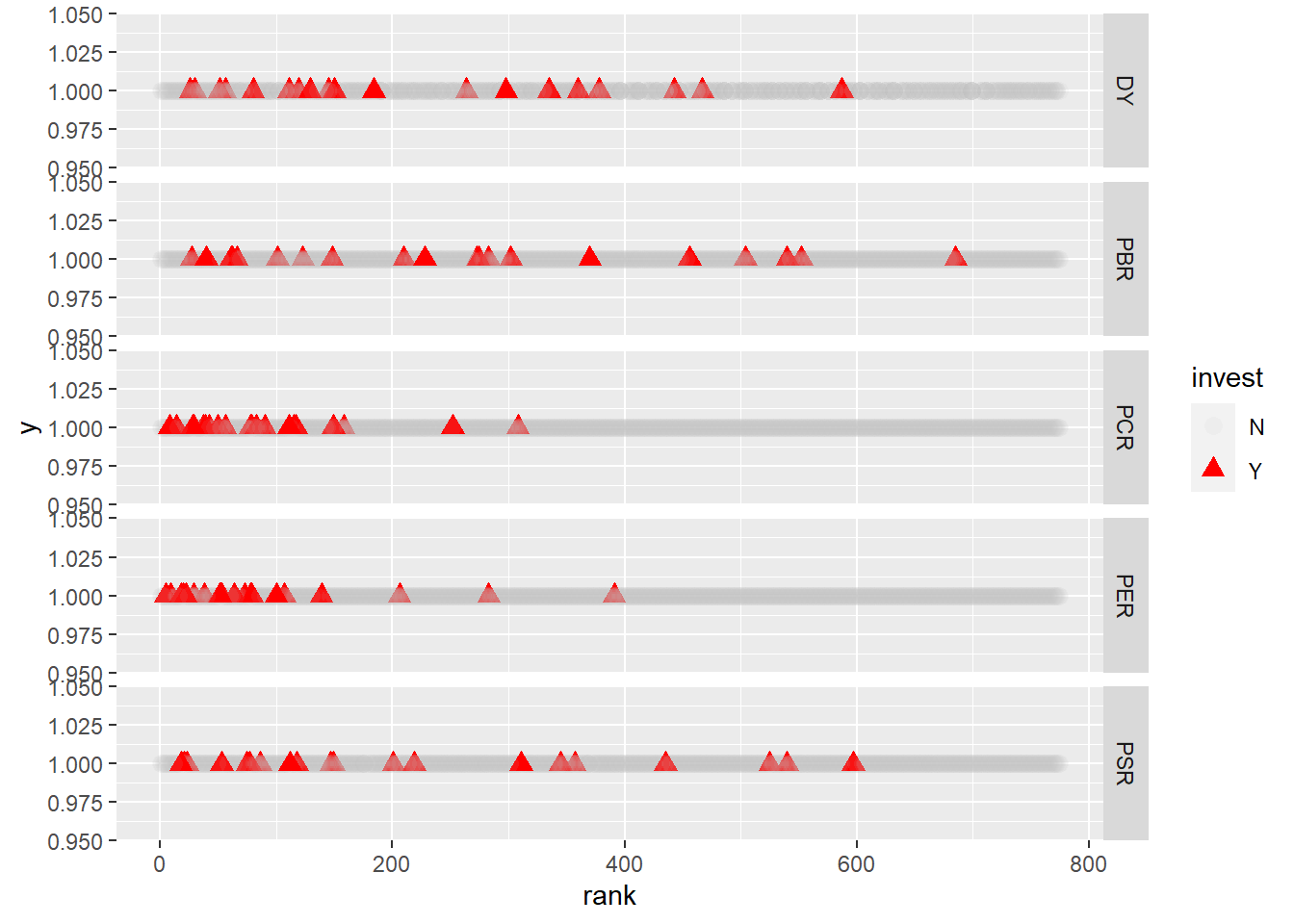
%>% select (DY, PBR, PER, PCR, PSR, invest) %>% na.omit () %>% pivot_longer (- invest) %>% group_by (name) %>% mutate (rank = ifelse (name == 'DY' , min_rank (desc (value)), min_rank (value))) %>% ggplot (aes (x = rank, y = 1 , shape = invest, color = invest, alpha = invest)) + geom_point (size = 3 ) + scale_color_manual (values= c ("grey" , "red" )) + facet_grid (name~ .)
Warning: Using alpha for a discrete variable is not advised.
밸류 지표 역시 멀티팩터 기준으로 선정된 종목들의 순위가 높습니다. 그러나 사용되는 지표가 많은 만큼 일부 지표에서는 순위가 낮은 종목들이 선정되기도 합니다.
이번에는 모멘텀 지표의 차이를 살펴보겠습니다.
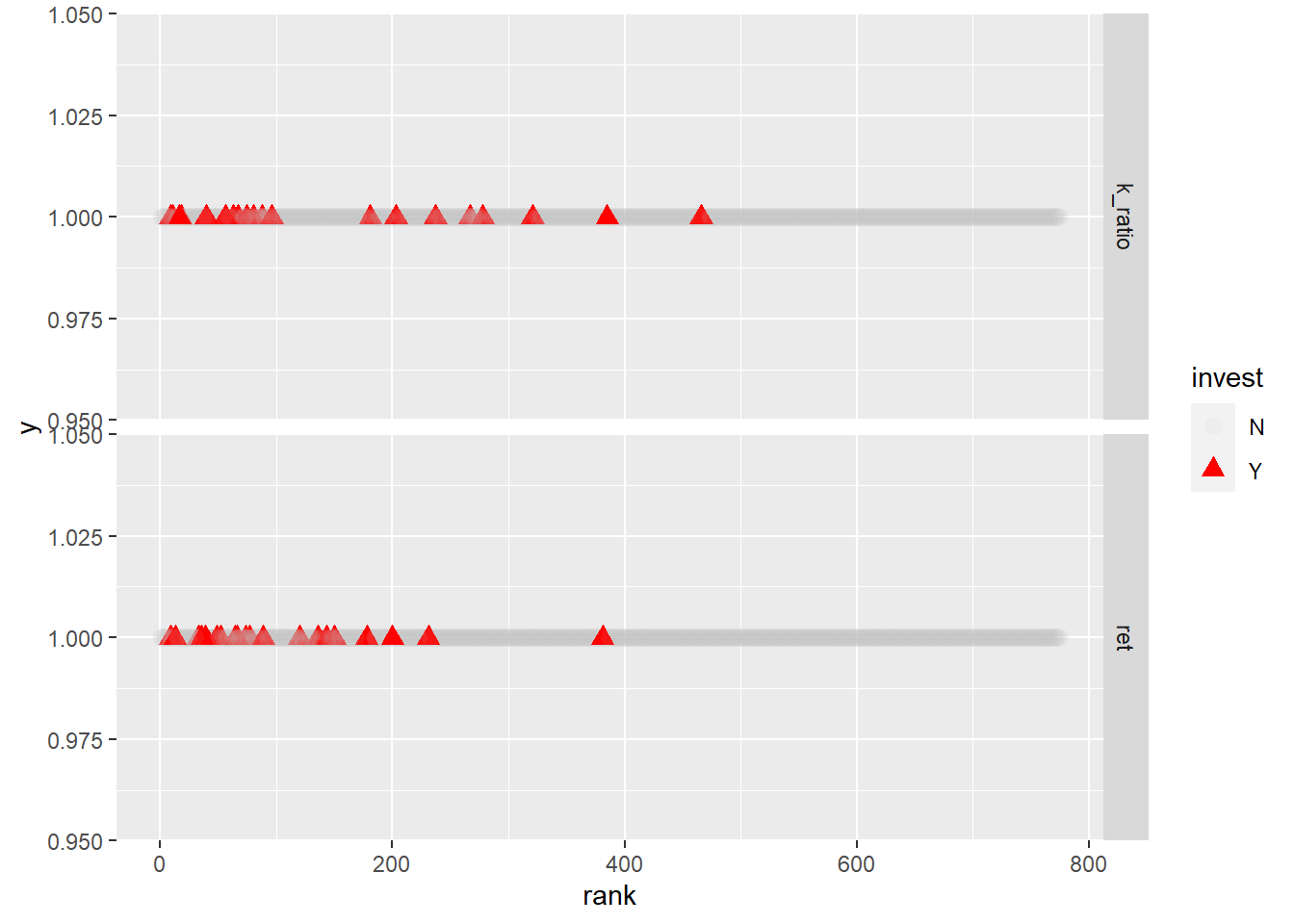
%>% select (ret, k_ratio, invest) %>% na.omit () %>% pivot_longer (- invest) %>% group_by (name) %>% mutate (rank = min_rank (desc (value))) %>% ggplot (aes (x = rank, y = 1 , shape = invest, color = invest, alpha = invest)) + geom_point (size = 3 ) + scale_color_manual (values= c ("grey" , "red" )) + facet_grid (name~ .)
Warning: Using alpha for a discrete variable is not advised.
모멘텀 지표 역시 멀티팩터 기준으로 선정된 종목들의 순위가 높습니다.
이처럼 멀티팩터 기준으로 종목을 선정할 경우 각 팩터가 골고루 좋은 종목을 선택할 수 있습니다. 이 외에도 팩터를 만들 수 있는 기본 데이터가 모두 있으므로 최근 적자기업 제외, 매출 증가 등 다양한 전략을 추가할 수도 있습니다.